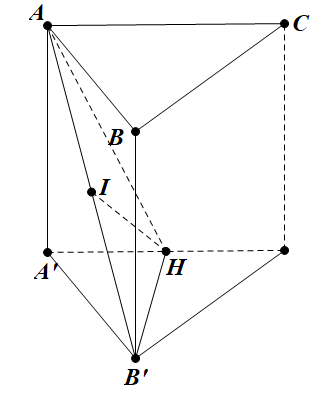
Cho hình lăng trụ tam giác đều \(A B C . A^{\prime} B^{\prime} C^{\prime} \text { có } A B=a\,và\,A A^{\prime}=\sqrt{2} a\). Góc giữa hai đường thẳng AB' và BC' bằng
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Gọi I, H lần lượt là trung điểm của AB' và A'C' . Khi đó IH là đường trung bình của \(\triangle A^{\prime} B C^{\prime} \text { nên } I H \| B C^{\prime} \Rightarrow\left(A B^{\prime}, B C^{\prime}\right)=\left(A B^{\prime}, I H\right)\)
\(\begin{aligned} &\text { Ta có } A B^{\prime}=a \sqrt{3}, B^{\prime} H=\frac{a \sqrt{3}}{2}, A H = \frac{3 a}{2} \text { nên } B^{\prime} H^{2}+H A^{2} =A B^{\prime 2}\\ &\text { hay } \triangle H A B^{\prime} \text { vuông tại } H \text { . } \end{aligned}\)
\(\begin{array}{l} I H=\frac{A B^{\prime}}{2}=\frac{a \sqrt{3}}{2} \Rightarrow \Delta B^{\prime} I H \text { đều, suy ra } \\ \left(A B^{\prime}, B C^{\prime}\right)=\left(A B^{\prime}, I H\right)=\widehat{B^{\prime} I H}=60^{\circ} . \end{array}\)
Câu hỏi liên quan
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
Góc giữa hai mặt phẳng (SAB) và (ABC) bằng:
-
Cho góc tam diện Sxyz với \(\widehat {xSy} = {120^0},\widehat {ySz} = {60^0},\widehat {zSx} = {90^0}\). Trên các tia Sx, Sy, Sz lần lượt lấy các điểm A, B, C sao cho SA = SB = SC = a. Góc giữa hai mặt phẳng (SAB) và (ABC) bằng :
-
Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. \(SA \bot \left( {ABCD} \right)\), SA = x. Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60o.
-
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và \(A B=\frac{a \sqrt{6}}{2}, A C=a \sqrt{2}, C D=a\). Gọi E là trung điểm của AD. Góc giữa hai đường thẳng AB và CE bằng
-
Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O. Các cạnh bên và các cạnh đáy đều bằng A. Gọi M là trung điểm SC. Góc giữa hai mặt phẳng (MBD) và (ABCD) bằng:
-
Cho hai mặt phẳng (P) và (Q) , a là một đường thẳng nằm trên (P). Mệnh đề nào sau đây sai?
-
Trong các mệnh đề sau đây, mệnh đề nào là đúng?
-
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và \(A B=\frac{a \sqrt{6}}{2}, A C=a \sqrt{2}, C D=a\). Gọi E là trung điểm của AD. Góc giữa hai đường thfẳng AB và CE bằng:
-
Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Người ta lấy trên giao tuyến d của hai mặt phẳng đó hai điểm A và B sao cho AB = 8. Gọi C là một điểm trên (P), D là một điểm trên (Q) sao cho AC, BD cùng vuông góc với giao tuyến d và AC = 6, BD = 24. Độ dài CD là:
-
Cho các mệnh đề sau với \((\alpha)\) và \((\beta)\) là hai mặt phẳng vuông góc với nhau với giao tuyến \(m = \left( \alpha \right) \cap \left( \beta \right)\) và a, b, c, d là các đường thẳng. Các mệnh đề sau, mệnh đề nào đúng?
-
Cho tứ diện ABCD có \(AB \bot \left( {BCD} \right)\). Trong \(\Delta BCD\) vẽ các đường cao BE và DF cắt nhau ở O. Trong (ADC) vẽ \(DK \bot AC\) tại K. Khẳng định nào sau đây sai ?
-
Cho hình chóp S.ABCD đáy ABCD là hình vuông cạnh a, \(\left( SAB \right)\bot \left( ABCD \right)\). H là trung điểm của AB, \(SH=HC,SA=AB\). Gọi a là góc giữa đường thẳng SC và mặt phẳng (ABCD). Giá trị của \(\tan \alpha \) là:
-
Tính cosin của góc giữa hai mặt của một tứ diện đều.
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Biết \(SO \bot \left( {ABCD} \right)\), \(SO = a\sqrt 3 \) và đường tròn ngoại tiếp ABCD có bán kính bằng a. Gọi \(\alpha\) là góc hợp bởi mặt bên (SCD) với đáy. Khi đó \(\tan \alpha = ?\)
-
Cho hình chóp cụt tứ giác đều ABCD.A'B'C'D' cạnh của đáy nhỏ ABCD bằng \(\frac{a}{3}\) và cạnh của đáy lớn A'B'C'D' bằng a. Góc giữa cạnh bên và mặt đáy bằng 60o. Tính chiều cao OO' của hình chóp cụt đã cho.
-
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = b, CC' = c. Độ dài đường chéo AC' là
-
Cho hình chóp S.ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD.
Hai mặt phẳng (SAB) và (SBC) vuông góc vì.
-
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\). Góc giữa hai đường thẳng AC và A'D bằng
-
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, tâm của đáy là O. Gọi M và N lần lượt là trung điểm của SA và BC. Biết rằng góc giữa MN và (ABCD) bằng 60o, cosin góc giữa MN và mặt phẳng (SBD) bằng :
