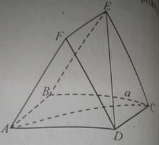
Cho hình chóp S.ABCD với ABCD là hình chữ nhật tâm O có \(AB = a,{\rm{ }}AD = 2a.{\rm{ }}SA\) vuông góc với đáy và SA = a. Gọi (P) là mặt phẳng qua SO và vuông góc với (SAD). Diện tích thiết diện của (P) và hình chóp S.ABCD bằng bao nhiêu?

Câu hỏi liên quan

• Cho hai hình vuông ABCD và ABEF cạnh a nằm trên hai mặt phẳng vuông góc. Tính DE.

  

• Cho các mệnh đề sau với \((\alpha)\) và \((\beta)\) là hai mặt phẳng vuông góc với nhau với giao tuyến \(m = \left( \alpha \right) \cap \left( \beta \right)\) và a, b, c, d là các đường thẳng. Các mệnh đề sau, mệnh đề nào đúng?

• Cho hai mặt phẳng (P) và (Q) , a là một đường thẳng nằm trên (P). Mệnh đề nào sau đây sai?

ZUNIA12

• Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. \(SA \bot \left( {ABCD} \right)\), SA = x. Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60^o.

• Cho ba tia Ox, Oy, Oz vuông góc nhau từng đôi một. Trên Ox, Oy, Oz lần lượt lấy các điểm A, B, C sao cho OA = OB = OC = a. Khẳng định nào sau đây sai?

• Cho hình chóp S.ABCD có đáy ABCD là hình vuông và \(S A \perp(A B C D)\), gọi O là tâm hình vuông ABCD . Khẳng định nào sau đây sai?

• Cho hình chóp S.ABC có tất cả các cạnh đều bằng a. Gọi I, J lần lượt là trung điểm của SA, BC. Tính số đo của góc hợp bởi IJ và SB.

• Cho hình chóp tứ giác đều S.ABCD đáy ABCD là hình vuông, E là điểm đối xứng với D qua trung điểm SA. Gọi M, N lần lượt là trung điểm của AE và BC. Góc giữa hai đường thẳng MN và BD bằng:

• Hình hộp ABCD.A'B'C'D' trở thành hình lăng trụ tứ giác đều khi phải thêm các điều kiện nào sau đây?

• Cho tứ diện  ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và \(A B=\frac{a \sqrt{6}}{2}, A C=a \sqrt{2}, C D=a\). Gọi E là trung điểm của AD. Góc giữa hai đường thfẳng AB và CE bằng:

• Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính của góc giữa một mặt bên và một mặt đáy.

• Cho hình lăng trụ đứng ABC.A'B'C' có AB = AA' = a, BC = 2a, \(CA = a\sqrt 5 \). Khẳng định nào sau đây sai?

• Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, AC = 2a. Các cạnh bên vuông góc với đáy và AA' = a. Khẳng định nào sau đây sai ?

• Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích của hình chóp S.ABCD là \(\frac{{{a}^{3}}\sqrt{15}}{6}\). Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) là:

• Cho hình lăng trụ tam giác đều \(A B C . A^{\prime} B^{\prime} C^{\prime} \text { có } A B=a\,và\,A A^{\prime}=\sqrt{2} a\). Góc giữa hai đường thẳng AB' và BC' bằng

• Cho hình chóp S.ABCD, đáy ABCD là hình vuông, \(SA \bot (ABCD)\). Gọi \((\alpha)\) là mặt phẳng chứa AB và vuông góc với (SCD), \((\alpha)\) cắt chóp S.ABCD theo thiết diện là hình gì?

• Cho hình chóp S.ABCD có đáy ABCD là hình vuông và \(SA \bot \left( {ABCD} \right)\), gọi O là tâm hình vuông ABCD. Khẳng định nào sau đây sai?

• Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc \(\widehat {BAD} = {60^0}\). Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và \(SO = \frac{{3a}}{4}\). Gọi E là trung điểm BC và F là trung điểm BE. Góc giữa hai mặt phẳng (SOF) và (SBC) là

• Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC). Khẳng định nào sau đây sai ?

• Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. AB = 2a, AD = DC = a. Cạnh bên SA vuông góc với đáy và \(SA = a\sqrt 2 \). Chọn khẳng định sai trong các khẳng định sau?