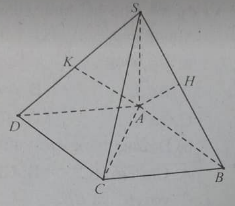
Cho hình chóp tam giác đều S.ABC với SA = 2AB. Góc giữa (SAB) và (ABC) bằng a. Chọn khẳng định đúng trong các khẳng định sau?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai.png)
Gọi O là tâm của tam giác đều ABC
Gọi \(CO \cap AB = H\) suy ra H là trung điểm AB(\(\Delta ABC\) vì đều)
\( \Rightarrow OH \bot AB\) và \(OH = \frac{1}{3}CH = \frac{1}{3}.\frac{{AB\sqrt 3 }}{2} = \frac{{AB\sqrt 3 }}{6}\)
Tìm góc giữa (SAB) và (ABC)
\(\left\{ {\begin{array}{*{20}{c}} {\left( {SAB} \right) \cap \left( {ABC} \right) = AB}\\ {OH \bot AB}\\ {SO \bot AB{\rm{ }}\left( {SO \bot (ABC)} \right){\rm{ }}} \end{array}} \right.\)
\(\Rightarrow SH \bot AB\) (1)
Ta có
\(\left\{ {\begin{array}{*{20}{c}} {\left( {SAB} \right) \cap \left( {ABC} \right) = AB}\\ {OH \bot AB,{\rm{ }}OH \subset (ABC)}\\ {SH \bot AB,SH \subset (SAB){\rm{ }}} \end{array}} \right.\)
\( \Rightarrow \left( {\widehat {(SAB);(ABC)}} \right) = \left( {\widehat {SH;OH}} \right) = \widehat {SHO} = \alpha \)
Từ (1) suy ra \(SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {{{\left( {2AB} \right)}^2} - {{\left( {\frac{{AB}}{2}} \right)}^2}} = \frac{{\sqrt {15} }}{2}AB\)
Từ đó ta có : \(\cos \alpha = \frac{{OH}}{{SH}} = \frac{{\frac{{\sqrt 3 }}{6}AB}}{{\frac{{\sqrt {15} }}{2}AB}} = \frac{1}{{3\sqrt 5 }}\)