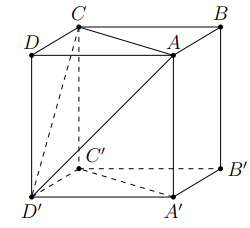
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) . Góc giữa \(A^{\prime} C^{\prime} \text { và } D^{\prime} C^{\prime}\) là
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai\(A^{\prime} C^{\prime} \| A C\) nên \(\widehat {\left( {{A^\prime }{C^\prime },{D^\prime }C} \right)} = \widehat {\left( {{D^\prime }C,AC} \right)}\)
Dễ thấy tam giác ACD0 là tam giác đều nên \(\widehat{D^{\prime} C A}=60^{\circ}\) do đó
\(\widehat {\left( {{A^\prime }{C^\prime },{D^\prime }C} \right)} = \widehat {\left( {{D^\prime }C,AC} \right)} = {60^\circ }\)
ADMICRO
YOMEDIA
ZUNIA9