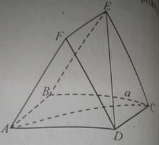
Cho hình chóp tứ giác đều S.ABCD, có đáy ABCD là hình vuông tâm O. Các cạnh bên và các cạnh đáy đều bằng A. Gọi M là trung điểm SC. Góc giữa hai mặt phẳng (MBD) và (ABCD) bằng:

Câu hỏi liên quan

• Cho hình lập phương ABCD. A’B’C’D’ có cạnh bằng a. Tính số đo góc giữa (BA’C) và (DA’C)

• Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng 60^o. Gọi M và N lần lượt là trung điểm của AB và CD.

  Góc giữa hai mặt phẳng (ACD) và (BCD) là:

• Cho hình chóp S,ABC có \(SA \bot \left( {ABC} \right)\) và \(AB \bot BC\), gọi I là trung điểm BC. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc nào sau đây?

ZUNIA12

• Cho hình chóp S.ABC có đường cao SA bằng 2a, tam giác ABC vuông ở C có \(AB=2a,\) \(\widehat{CAB}={{30}^{0}}\). Gọi H là hình chiếu vuông của A trên SC. Tính theo a thể tích của khối chóp H.ABC. Tính cô-sin của góc giữa hai mặt phẳng \(\left( SAB \right),\,\,\left( SBC \right).\)

• Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và \(A B=\frac{a \sqrt{6}}{2}, A C=a \sqrt{2}, C D=a\). Gọi E là trung điểm của AD. Góc giữa hai đường thẳng AB và CE bằng

• Cho hình chóp S.ABCD, đáy ABCD là hình vuông, \(SA \bot (ABCD)\). Gọi \((\alpha)\) là mặt phẳng chứa AB và vuông góc với (SCD), \((\alpha)\) cắt chóp S.ABCD theo thiết diện là hình gì?

• Cho hai đường thẳng chéo nhau a và b đồng thời \(a \bot b\). Chỉ ra mệnh đề đúng trong các mệnh đề sau:

• Cho hình lăng trụ đứng \(ABC.ABC\) có đáy là tam giác cân với \(AB=AC=a,\) góc \(\widehat{ABC}={{120}^{0}},\) cạnh bên BB’ = a. Gọi I là trung điểm của CC’. Tính cosin của góc giữa hai mặt phẳng (ABC) và (AB’I)?

• Trong lăng trụ đều, khẳng định nào sau đây sai?

• Trong các mệnh đề sau, mệnh đề nào sai? 

• Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝

  

  Tan của góc giữa mặt bên và mặt đáy bằng:

• Cho hai hình vuông ABCD và ABEF cạnh a nằm trên hai mặt phẳng vuông góc. Đường thẳng DE vuông góc?

  

• Cho hình chóp tam giác đều S.ABC với SA = 2AB. Góc giữa (SAB) và (ABC) bằng a. Chọn khẳng định đúng trong các khẳng định sau?

• Hình hộp ABCD.A'B'C'D' là hình hộp gì nếu tứ diện AA'B'D' có các cạnh đối vuông góc.

• Cho hình chóp S.ABCD có hai mặt bên (SAB) và (SAC) vuông góc với mặt phẳng (ABC), tam giác ABC vuông cân ở A và có đường cao AH \(\left( {H \in BC} \right)\). Gọi O là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây sai ?

• Mệnh đề nào sau đây là đúng?

• Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.

  Mặt phẳng (ABCD) vuông góc với mặt phẳng:

• Cho hai mặt phẳng (P) và (Q) , a là một đường thẳng nằm trên (P). Mệnh đề nào sau đây sai?

• Cho hai hình vuông ABCD và ABEF cạnh a nằm trên hai mặt phẳng vuông góc. Tính DE.

  

• Trong các mệnh đề sau, mệnh đề nào đúng?