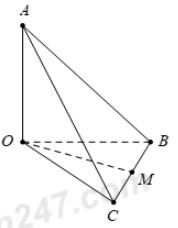
Cho hình chóp S.ABC có tất cả các cạnh đều bằng a. Gọi I, J lần lượt là trung điểm của SA, BC. Tính số đo của góc hợp bởi IJ và SB.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Gọi M là trung điểm của AB. Khi đó IM là đường trung bình của tam giác SAB nên IM//SB \(\Rightarrow (I J, S B)=(I J, I M)\)
Lại có \(I M=\frac{S B}{2}=\frac{a}{2} . \text { Tương tự } M J=\frac{a}{2} \text { . }\)
Mặt khác, dễ dàng chứng minh tam giác IBJ vuông tại J nên
\(I J=\sqrt{I B^{2}-I B^{2}}=\sqrt{\left(\frac{a \sqrt{3}}{2}\right)^{2}-\left(\frac{a}{2}\right)^{2}}=\frac{a \sqrt{2}}{2}\)
\(\Delta IM J \text { có } M I=M J=\frac{a}{2}, I J=\frac{a \sqrt{2}}{2}\) nên là tam giác vuông cân tại M. Suy ra
\((I J, S B)=(I J, I M)=\widehat{M I J}=45^{\circ}\)
Câu hỏi liên quan
-
Trong các mệnh đề sau, mệnh đề nào đúng?
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD) vì:
-
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng
-
Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có ACC'A' là hình vuông, cạnh bằng a. Cạnh đáy của hình lăng trụ bằng:
-
Trong các mệnh đề sau, mệnh đề nào đúng?
-
Cho ba tia Ox, Oy, Oz vuông góc nhau từng đôi một. Trên Ox, Oy, Oz lần lượt lấy các điểm A, B, C sao cho OA = OB = OC = a. Khẳng định nào sau đây sai?
-
Cho hình lập phương \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\). Góc giữa hai đường thẳng AC và A'D bằng
-
Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a, CD = 2x. Tính AB theo a và x?
-
Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc \(\widehat {BAD} = {60^0}\). Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và \(SO = \frac{{3a}}{4}\). Gọi E là trung điểm BC và F là trung điểm BE. Góc giữa hai mặt phẳng (SOF) và (SBC) là
-
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và \(A B=\frac{a \sqrt{6}}{2}, A C=a \sqrt{2}, C D=a\). Gọi E là trung điểm của AD. Góc giữa hai đường thẳng AB và CE bằng
-
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích của hình chóp S.ABCD là \(\frac{{{a}^{3}}\sqrt{15}}{6}\). Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) là:
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Biết \(SO \bot \left( {ABCD} \right)\), \(SO = a\sqrt 3 \) và đường tròn ngoại tiếp ABCD có bán kính bằng a. Gọi \(\alpha\) là góc hợp bởi mặt bên (SCD) với đáy. Khi đó \(\tan \alpha = ?\)
-
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có cạnh đáy bằng \(2a\sqrt 3 \) và cạnh bên bằng 2a. Gọi G và G' lần lượt là trọng tâm của hai đáy ABC và A'B'C'. Khẳng định nào sau đây đúng khi nói về AA'G'G?
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ABCD). Gọi H là trung điểm của AB, \(SH=HC,SA=AB\). Gọi \(\alpha \) là góc giữa đường thẳng SC và mặt phẳng (ABCD). Giá trị của \(\tan \alpha \) là:
-
Cho hình lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng a, góc giữa hai mặt phẳng (ABCD) và (ABC') có số đo bằng 60o. Cạnh bên của hình lăng trụ bằng:
-
Tứ diện đều ABCD cạnh a, M là trung điểm của cạnh CD. Cô-sin của góc giữa AM và BD là
-
Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng a và góc \(\widehat A = {60^0}\), cạnh \(SC = \frac{{a\sqrt 6 }}{2}\) và SC vuông góc với mặt phẳng (ABCD). Trong tam giác SCA kẻ \(IK \bot SA\) tại K. Tính độ dài IK được
-
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝
Tan của góc giữa mặt bên và mặt đáy bằng:
-
Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a, CD = 2x. Gọi I, J lần lượt là trung điểm của AB và CD. Tính IJ theo a và x?
-
Tính cosin của góc giữa hai mặt của một tứ diện đều.
