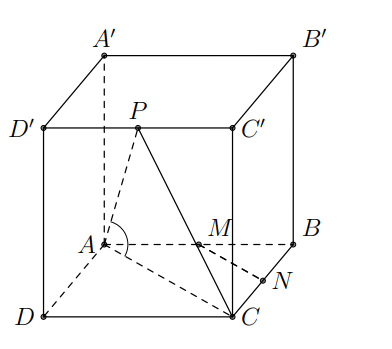
Cho hình lập phương \(A B C D . A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) cạnh a.Gọi M, N, P lần lượt là trung điểm các cạnh A B, B C, C'D'. Xác định góc giữa hai đường thẳng MN và AP.
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiDo AC song song với MN nên góc giữa hai đường thẳng MN và AP bằng góc giữa hai đường thẳng AC và AP.
Tính được \(P C=\frac{a \sqrt{5}}{2} ; A P=\frac{3 a}{2} ; A C=a \sqrt{2} .\)
Áp dụng định lý cosin cho tam giác ACP ta có
\(\begin{array}{l} \cos \widehat{C A P}=\frac{A P^{2}+A C^{2}-P C^{2}}{2 A P \cdot A C}=\frac{\frac{9 a^{2}}{4}+2 a^{2}-\frac{5 a^{2}}{4}}{2 \cdot \frac{3 a}{2} \cdot a \sqrt{2}}=\frac{\sqrt{2}}{2} \\ \Rightarrow \widehat{C A P}=45^{\circ} . \end{array}\)
ADMICRO
YOMEDIA
ZUNIA9