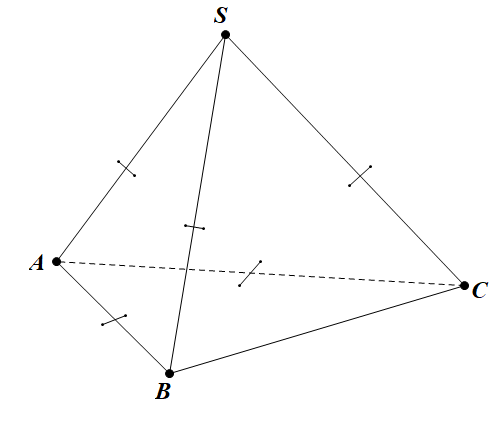
Cho hình chóp S.ABC có SA = SB = SC = AB = AC = 1, \(B C=\sqrt{2}\). Tính góc giữa hai đường thẳng AB, SC
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(A B^{2}+A C^{2}=2=B C^{2} \Rightarrow \Delta A B C\) vuông tại A.
\(\begin{aligned} \cos (\overrightarrow{A B}, \overrightarrow{S C}) &=\frac{\overrightarrow{A B} \cdot \overrightarrow{S C}}{|\overrightarrow{A B}| \cdot|\overrightarrow{S C}|}=\frac{\overrightarrow{A B}(\overrightarrow{A C}-\overrightarrow{A S})}{1 \cdot 1} \\ &=\overrightarrow{A B} \overrightarrow{A C}-\overrightarrow{A B} \overrightarrow{A S} \\ &=0-1 \cdot 1 \cdot \cos 60^{\circ}\\ &=-\frac{1}{2} \end{aligned}\)
Suy ra \((\overrightarrow{A B}, \overrightarrow{S C})=120^{\circ}\)
Do đó góc giữa hai đường thẳng AB và SC bằng \(180^{\circ}-120^{\circ}=60^{\circ}\)