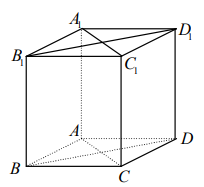
Cho hình lập phương \(A B C D \cdot A_{1} B_{1} C_{1} D_{1}\) . Chọn khẳng định sai?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\begin{array}{l} \text { Ta có: } \overrightarrow{A A_{1}} \cdot \overrightarrow{B_{1} D_{1}}=\overrightarrow{B B_{1}} \cdot \overrightarrow{B D}=\overrightarrow{B B_{1}} \cdot(\overrightarrow{B A}+\overrightarrow{B C})\\ =\overrightarrow{B B_{1}} \cdot \overrightarrow{B A}+\overrightarrow{B B_{1}} \cdot \overrightarrow{B C}=0 \end{array}\)
\(\left(\text { vì }\left(\overrightarrow{B B_{1}}, \overrightarrow{B A}\right)=90^{0} \text { và }\left(\overrightarrow{B B_{1}}, \overrightarrow{B C}\right)=90^{0}\right)\)
Do đó \(\left(\overrightarrow{A A_{1}}, \overrightarrow{B_{1} D_{1}}\right)=90^{0} \Rightarrow\left(A A_{1}, B_{1} D_{1}\right)=90^{0}\)