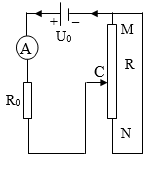
Cho mạch điện (như hình vẽ):
.png)
AB làm biến trở con chạy C có điện trở toàn phần là 120Ω. Nhờ có biến trở làm thay đổi cường độ dòng điện trong mạch từ 0.9A đến 4.5A. Tính công suất toả nhiệt lớn nhất trên biến trở. Biết U không đổi.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiKhi đó công suất toả nhiệt: \({P_x}\; = {\rm{ }}{R_x}.{I^2}\)
\({P_x}\; = {\rm{ }}{R_x}.\frac{{{U^2}}}{{{{({R_1} + {R_x})}^2}}} = \frac{{{U^2}.{R_x}}}{{{R^2}_1 + 2{R_1}{R_x} + {R^2}_x}} = \frac{{{U^2}}}{{\frac{{{R^2}_1}}{{{R_x}}} + 2{R_1} + {R_x}}}\)
Để Px đạt giá trị lớn nhất ⇔ \({\frac{{{R^2}_1}}{{{R_x}}} + {R_x}}\) nhỏ nhất.
Áp dụng bất đẳng thức Cô si vào 2 số dương ta có:
\(\frac{{{R^2}_1}}{{{R_x}}} + {R_x} \ge 2.\sqrt {\frac{{{R^2}_1}}{{{R_x}}}{R_x}} = 2\sqrt {{R_1}^2} = 2{R_1}\)
Nghĩa là: giá trị nhỏ nhất là 2R1, thay R1 = 30(Ω)
Ta có phương trình:
\(\frac{{{{30}^2}}}{{{R_x}}} + {R_x} = 60\; \Leftrightarrow {\rm{ }}{R_x}^2\; - {\rm{ }}60{R_x}\; + {\rm{ }}900{\rm{ }} = {\rm{ }}0{\rm{ }} \Leftrightarrow {\rm{ }}{R_x}\; = {\rm{ }}30\Omega \)
Khi đó Px (cực đại) là:
\({P_{max}} = \frac{{{U^2}.{R_x}}}{{{{\left( {{R_1} + {R_x}} \right)}^2}}} = \frac{{{{30.135}^2}}}{{{{(30 + 30)}^2}}} = 151,875\)W
Câu hỏi liên quan
-
Công suất của một bếp điện thay đổi thế nào khi hiệu điện thế đặt vào hai đầu bếp giảm đi còn một nửa?
-
Công thức nào sau đây không đúng?
-
Trên hai bóng đèn có ghi (220V - 60W ) và (220V - 75W ). Biết rằng dây tóc của hai bóng đèn này đều bằng vônfram và có tiết diện bằng nhau. Dây tóc của đèn nào có độ dài lớn hơn và lớn hơn bao nhiêu lần?
-
Một bàn là ghi 220V - 1000W. Tính điện trở và cường độ dòng điện định mức của bàn là
-
Hai bóng đèn giống nhau loại (12V-12W) mắc song song nhau vào hai điểm có hiệu điện thế 12V. Công suất tiêu thụ của các đèn là:
-
Trên một bóng đèn có ghi 110V - 55W. Điện trở của nó là
-
Trên bóng đèn Đ1, Đ2 có ghi số tương ứng là 3V - 1,2W và 6V - 6W. Cần mắc hai đèn này cùng với một biến trở vào hiệu hiệu điện thế U = 9V để hai đèn sáng bình thường. Cần ắmc hai đèn và biến trở như thế nào để thỏa mãn yêu cầu của đề bài?
-
Hai bóng đèn lần lượt có ghi số 12V - 9W và 12V - 6W được mắc song song vào nguồn điện có hiệu điện thế 12V.
-
Cho mạch điện (như hình vẽ).
Biết Uo = 12 V, Ro là điện trở, R là biến trở ampe kế lí tưởng. Khi con chạy C của biến trở R từ M đến N, ta thấy ampe kế chỉ giá trị lớn nhất I1 = 2A. Và giá trị nhỏ nhất I2 = 1A. Bỏ qua điện trở của các dây nối. Xác định vị trí của con chạy C của biến trở R để công suất tiêu thụ trên toàn biến trở bằng một nửa công suất cực đại của nó
-
Công thức nào sau đây không phải là công thức tính công suất?
-
Trên một bóng đèn có ghi Đ (6V - 6W). Khi mắc đèn vào hai điểm có U = 3V thì công suất tiêu thụ của đèn là:
-
Cho mạch điện như hình vẽ. Biến trở AB là một dây dẫn đồng chất, chiều dài l = 1,3 m, tiết diện thẳng S = 0,1 mm2, điện trở suất ρ = 10-6 Ω.m. U là hiệu điện thế không đổi. Di chuyển con chạy C ta nhận thấy khi ở các vị trí cách đầu A một đoạn 10 cm hoặc cách đầu B một đoạn 40 cm thì công suất toả nhiệt trên biến trở là như nhau. Gọi công suất tỏa nhiệt trên R0 ứng với 2 vị trí của con chạy C kể trên lần lượt là P1 và P2. Tìm tỷ số P1/P2.
.png)
-
Một nguồn điện có suất điện động 12 V. Khi mắc nguồn này với một bóng đèn tạo thành mạch điện kín thì dòng điện chạy qua nó có cường độ 0,9 A. Công của nguồn điện sản ra trong thời gian 15 phút và công suất của nguồn lần lượt là
-
Một quạt điện dùng trên xe có ghi 12V-15W. Mắc quạt vào hiệu điện thế 12V cho rằng hiệu suất của quạt là 85%, tính điện trở của quạt?
-
Trên một bóng đèn có ghi (110V - 45 W). Tính cường độ dòng điện qua bóng đèn này khi đèn sáng bình thường và điện trở của đèn khi đó.
-
Trên hai bóng đèn có ghi 220V - 100W và 220V - 40W. Biết dây tóc của hai bóng đèn này đều bằng Vonfram và có tiết diện bằng nhau. Gọi l1 và l2 là chiều dài của dây tóc mỗi bóng đèn, tỉ số giữa chúng là
-
Một bóng đèn có ghi 220V-100W. Nếu mắc đèn vào nguồn điện có HĐT 110V thì công suất của tiêu thụ của đèn là bao nhiêụ
-
Cho sơ đồ mạch điện như hình 4: đặt vào hai đầu đoạn mạch A, B hiệu điện thế không đổi UAB = 24 V, biến trở PQ có điện trở toàn phần R0 = 25 Ω, các điện trở có giá trị R1 = 24 Ω, R2 = 7 Ω. Bỏ qua điện trở của dây nối và khoá K. Khi khoá K mở: di chuyển con chạy C thì nhận thấy khi \(\frac{{CP}}{{CQ}} = \frac{6}{{19}}\) thì công suất trên biến trở lớn nhất. Xác định số chỉ của ampe kế A và công suất toàn mạch khi đó.
.png)
-
Một bếp điện khi hoạt động bình thường có điện trở R = 80\(\Omega\)và cường độ dòng điện qua bếp khi đó là I = 2,5 A. Dùng bếp điện trên để đun sôi 1,5l nước có nhiệt độ ban đầu 25oC thì thời gian đun nước là 20 phút. Coi rằng nhiệt lượng cung cấp để đun sôi nước là có ích. Tính hiệu suất của bếp. Cho biết nhiệt dung riêng của nước là c = 4200J/kg.K
-
Nếu giảm hiệu điện thế ở hai đầu đường dây tải điện lên 100 lần thì công suất hao phí vì toả nhiệt trên đường dây dẫn sẽ:
