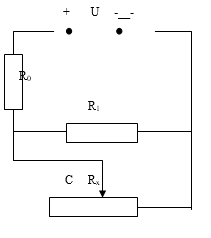
Cho mạch điện (như hình vẽ).

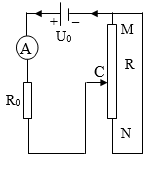
Biết Uo = 12 V, Ro là điện trở, R là biến trở ampe kế lí tưởng. Khi con chạy C của biến trở R từ M đến N, ta thấy ampe kế chỉ giá trị lớn nhất I₁ = 2A. Và giá trị nhỏ nhất I₂ = 1A. Bỏ qua điện trở của các dây nối. Xác định vị trí của con chạy C của biến trở R để công suất tiêu thụ trên toàn biến trở bằng một nửa công suất cực đại của nó

A. có 2 vị trí của con chạy C trên biến trở R sao cho R_MC = 11 Ω hoặc R_MC= 23 Ω

B. có 2 vị trí của con chạy C trên biến trở R sao cho R_MC = 12 Ω hoặc R_MC= 11 Ω

C. có 2 vị trí của con chạy C trên biến trở R sao cho R_MC = 1 Ω hoặc R_MC=11 Ω

D. có 2 vị trí của con chạy C trên biến trở R sao cho R_MC = 1 Ω hoặc R_MC= 23 Ω

Suy nghĩ và trả lời câu hỏi trước khi xem đáp án

Môn: Vật Lý Lớp 9

Chủ đề: Điện học

Bài: Công suất điện

Lời giải:

Báo sai

Để có phương án giải phần này ta phải áp dụng công thức P = I²R và định luật bảo toàn năng lượng trên toàn mạch điện .

Đặt \({R_{MNC}} = y = \frac{{x(24 - x)}}{{24}}\)

Mà P_MNC = R_MNC.I²

Công suất tiêu thụ trên toàn biến trở là:

\(P = y.{I^2} = {\left( {\frac{{{U_o}}}{{{R_o} + y}}} \right)^2}.y = {\left( {\frac{{12}}{{6 + y}}} \right)^2}.y\)

Mà công suất của nguồn điện và công suất tiêu thụ trên R₀ là \(\;{P_n}\; = {\rm{ }}{U_o}I{\rm{ }};{\rm{ }}{P_{{R_o}}}\; = {\rm{ }}{R_o}.{I^2}\)

Theo định luật bảo toàn năng lượng ta có: \({P_n}\; = {P_{{R_o}}}\; + P\;{\rm{ }}\;hay\;{\rm{ }}\;{U_o}I = {R_o}.{I^2}\; + P\)

\(\Rightarrow {\rm{ }}{R_0}.{I^2}\;-{\rm{ }}{U_0}.I{\rm{ }} + {\rm{ }}P{\rm{ }} = {\rm{ }}0{\rm{ }}\left( * \right)\)

(*) là phương trình bậc 2 với ẩn là I

Để phương trình có nghiệm: Δ ≥ 0

\(\Rightarrow {\rm{ }}\Delta {\rm{ }} = {\rm{ }}{U^2}\; - {\rm{ }}4{R_0}.P{\rm{ }} \ge {\rm{ }}0\; \Rightarrow P \le \frac{{{U_o}^2}}{{4{R_0}}}\)

Vậy \(\begin{array}{l} {P_{\max }} = \frac{{{U_o}^2}}{{4{R_0}}} = \frac{{{{12}^2}}}{{4.6}} = 6W\\ \Rightarrow {\rm{ }}{\left( {\frac{{12}}{{6 + y}}} \right)^2}.y = \frac{{{P_{\max }}}}{2} = 3\\ \Leftrightarrow \frac{{144y}}{{36 + 12y + {y^2}}} = 3\\ \begin{array}{*{20}{l}} { \Leftrightarrow {\rm{ }}144y{\rm{ }} = {\rm{ }}108{\rm{ }} + {\rm{ }}36y{\rm{ }} + {\rm{ }}3{y^2}}\\ { \Leftrightarrow {\rm{ }}3{y^2}\; - {\rm{ }}108y{\rm{ }} + {\rm{ }}108{\rm{ }} = {\rm{ }}0} \end{array}\\ \Leftrightarrow {\rm{ }}{y^2}\; - {\rm{ }}36y{\rm{ }} + {\rm{ }}36{\rm{ }} = {\rm{ }}0\\ \Leftrightarrow \left[ \begin{array}{l} {y_1} \approx 35(loai)\\ {y_2} \approx 1\Omega \end{array} \right. \end{array}\)

Mà ta đặt \(y = \frac{{x(24 - x)}}{{24}}\) nên ta có phương trình:

\(y = \frac{{x(24 - x)}}{{24}} = 1 \Rightarrow {\rm{ }}{x^2}\; - {\rm{ }}24x{\rm{ }} + {\rm{ }}24{\rm{ }} = {\rm{ }}0\)

Giải phương trình trên ta có x₁ = 1 Ω; x₂ = 23 Ω.

Vậy có 2 vị trí của con chạy C trên biến trở R sao cho R_MC = 1 Ω hoặc R_MC= 23 Ω thì công suất tiêu thụ trên toàn biến trở bằng một nửa công suất cực đại của nó.