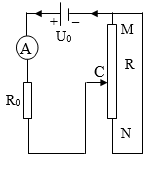
Cho mạch điện như hình vẽ.
.png)
Đèn Đ có ghi: 6 V – 3 W. Thay đổi biến trở R để công suất trên nó đạt giá trị cực đại và bằng 9 W, khi đó đèn sáng bình thường. Tìm giá trị của R0 và U. Bỏ qua điện trở của dây nối.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐiện trở của đèn là: Rđ = 12 Ω, đặt R = x.
Điện trở tương đương của mạch:
\({R_{td}} = \frac{{12x}}{{12 + x}} + {R_o} = \frac{{(12 + {R_o})x + 12{R_o}}}{{12 + x}}\)
Cường độ dòng điện trong mạch:
\(I = \frac{U}{{{R_{td}}}} = \frac{{U(12 + x)}}{{(12 + {R_o})x + 12{R_o}}}\)
Cường độ dòng điện qua biến trở:
\({I_x} = I\frac{{12}}{{x + 12}} = \frac{{U(12 + x)}}{{(12 + {R_o})x + 12{R_o}}}\)
Công suất trên biến trở:
\(\begin{array}{l} {P_x} = {I^2}_xx = \frac{{{{12}^2}{U^2}x}}{{{{\left[ {(12 + {R_o})x + 12{R_o}} \right]}^2}}}\\ \Rightarrow {P_x} = \frac{{{{12}^2}{U^2}}}{{{{\left[ {(12 + {R_o})\sqrt x + \frac{{12{R_o}}}{{\sqrt x }}} \right]}^2}}} \le \frac{{{{12}^2}{U^2}}}{{4.12.{R_o}(12 + {R_o})}} = \frac{{3{U^2}}}{{{R_o}(12 + {R_o})}} = 9W\\ \Rightarrow {\rm{ }}{U^2}\; = {\rm{ }}3.{R_0}(12{\rm{ }} + {\rm{ }}{R_0}){\rm{ }}\left( 1 \right) \end{array}\)
Dấu “ = ” xảy ra khi \(x = \frac{{12{R_0}}}{{(12{\rm{ }} + {\rm{ }}{R_0})}}\)
Khi đèn sáng bình thường thì hiệu điện thế hai đầu biến trở bằng hiệu điện thế hai đầu đèn bằng 6 V
\(\frac{{12U}}{{(12 + {R_o})x + 12{R_o}}}.\frac{{12{R_o}}}{{12 + {R_o}}} = \frac{{12U}}{{(12 + {R_o})\frac{{12{R_o}}}{{12 + {R_o}}} + 12{R_o}}}.\frac{{12{R_o}}}{{12 + {R_o}}} = 6\)
Hay: U = 12 + R0 (2)
Từ (1) và (2) suy ra: R0 = 6 Ω và U = 18 V.
Câu hỏi liên quan
-
Công thức nào sau đây không phải là công thức tính công của dòng điện?
-
Giữa hai điểm có hiệu điện thế U = 220V người ta mắc song song hai dây kim loạị. Cường độ dòng điện qua dây thứ nhất là I1 = 4A và qua dây thứ hai là I2 = 2A. Tính công suất của đoạn mạch trên.
-
Có hai bóng đèn có ghi 110V - 60W và một quạt điện loại 220V - 100W, mắc 2 đèn nối tiếp, cả cụm song song với quạt. Nếu mỗi ngày đèn được thắp 6h và quạt sử dụng 5h thì trong 1 tháng (30 ngày), gia đình này tiệu thụ bao nhiêu điện năng? Tính tiền điện phải trả nếu mỗi số công tơ là 700đ.
-
Một bóng đèn có hiệu điện thế định mức 2,5V và cường độ dòng điện định mức 0,4A được mắc với một biến trở con chạy để sử dụng với nguồn điện có hiệu điện thế không đổi 12V. Nếu biến trở có điện trở lớn nhất là 40Ω thì khi đèn sáng bình thường dòng điện chạy qua bao nhiêu phần trăm (%) tổng số vòng dây của biến trở?
-
Trong các đèn sau đây khi được thắp sáng bình thường, thì bóng nào sáng mạnh nhất?
-
Một quạt điện hoạt động ở hiệu điện thế 220V, sản ra công cơ học Pc = 321W. Biết điện trở trong của động cơ là r = 4 Ω. Tính hiệu suất của động cơ.
-
Trên nhiều dụng cụ trong gia đình thường có ghi 220V và số Woát (W). Số Woát này có ý nghĩa gì?
-
Một gia đình dùng 5 bóng đèn loại 220V – 40W và một bếp điện 220V – 1000W. Mỗi ngày dùng 6 giờ. Trong một tháng (30 ngày) phải trả bao nhiêu tiền điện, biết giá mỗi số điện là 800 đồng, đèn được mắc vào mạch điện 220V.
-
Cho các dụng cụ sau: một nguồn điện có hiệu điện thế không đổi U = 12 V hai bóng đèn Đ1 (6 V - 0,4 A); Đ2 (6V - 0,1A) và một biến trở Rb. Có thể mắc chúng thành mạch như thế nào để hai đèn đều sáng bình thường vẽ sơ đồ mạch và tính điện trở của biến trở tương ứng với mỗi cách mắc đó.
-
Một bóng đèn loại 6V - 3W được mắc nối tiếp với điện trở R vào hiệu điện thế U = 9V thì bóng đèn sáng bình thường. Thông tin nào sau đây là sai?
-
Một ấm điện có hai dây dẫn R1 và R2 để đun nước. Nếu dùng dây R1 thì nước trong ấm sẽ sôi sau thời gian t1 = 10 (phút). Còn nếu dùng dây R2 thì nước sẽ sôi sau thời gian t2 = 40 (phút). Nếu dùng cả hai dây mắc song song thì nước sẽ sôi sau thời gian là:
-
Một bàn là điện có công suất định mức 1100W và cường độ dòng điện định mức 5A. điện trở suất là 1,1.10-6Wm và tiết diện của dây là 0,5mm2, chiều dài của dây là :
-
Cho mạch điện (như hình vẽ).
Biết Uo = 12 V, Ro là điện trở, R là biến trở ampe kế lí tưởng. Khi con chạy C của biến trở R từ M đến N, ta thấy ampe kế chỉ giá trị lớn nhất I1 = 2A. Và giá trị nhỏ nhất I2 = 1A. Bỏ qua điện trở của các dây nối. Xác định vị trí của con chạy C của biến trở R để công suất tiêu thụ trên toàn biến trở bằng một nửa công suất cực đại của nó
-
Trên bóng đèn có ghi 6V – 2W. Khi đèn sáng bình thường thì dòng điện chạy qua đèn có cường độ là:
-
Mạch nguồn có suất điện động E=6V, điện trở trong \(r=2\Omega\), mạch ngoài có điện trở R. Để công suất tiêu thụ ở mạch ngoài là 4W thì điện trở R phải có giá trị:
-
Một bóng đèn có hiệu điện thế định mức 2,5V và cường độ dòng điện định mức 0,4A được mắc với một biến trở con chạy để sử dụng với nguồn điện có hiệu điện thế không đổi 12V. Đèn và biến trở phải mắc với nhau như thế nào để đèn có thể sáng bình thường?
-
Công suất điện cho biết:
-
Một bàn là ghi 220V - 1000W. Người ta mắc bàn là nối tiếp với điện trở 1,6 Ω rồi mắc vào nguồn điện có hiệu điện thế 220V. Coi điện trở của bàn là không đổi. Hãy tính công suất của bàn là trong trường hợp này?
-
Trên bàn là có ghi 220V – 1100W. Khi bàn là này hoạt động bình thường thì nó có điện trở là bao nhiêu?
-
Một ấm nước dùng với hiệu điện thế 220V thì đun sôi được 1,5lít nước từ nhiệt độ 200C trong thời gian 10 phút. Biết nhiệt dung riêng của nước là 4200J/kg.K. Khối lượng riêng của nước là 1000kg/m3 và hiệu suất của ấm là 90%. Tính công suất điện của ấm.
