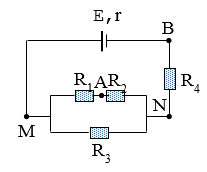
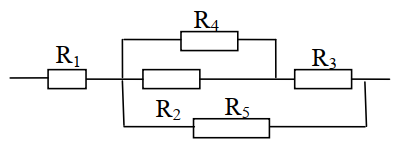
Cho mạch điện như hình vẽ: \(E = 24V , r = 1\Omega, R_1 = 3\Omega, R_2 = R_3 = R_4 = 6\Omega, R_A= 0 \). Tìm số chỉ của ampe kế.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
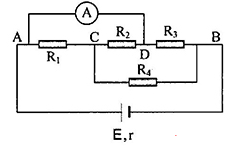
Báo saiVì ampe kế có điện trở không đáng kể nên A và D cùng điện thế, do đó chập A và D, mạch điện vẽ lại như hình:
+ Ta có, mạch gồm: \([[R_1//R_2]ntR_4]//R_3\)
\(\begin{array}{l} {R_{12}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{3.6}}{{3 + 6}} = 2\Omega \\ {R_{124}} = {R_{12}} + {R_4} = 2 + 6 = 8\Omega \end{array}\)
+ Điện trở tương đương của toàn mạch:
\( R = \frac{{{R_{124}}{R_3}}}{{{R_{124}} + {R_3}}} = \frac{{8.6}}{{8 + 6}} = \frac{{24}}{7}\Omega \)
+ Cường độ dòng điện chạy trong mạch chính:
\( I = \frac{E}{{{R_N} + r}} = \frac{{24}}{{\frac{{24}}{7} + 1}} = \frac{{168}}{{31}}A\)
+ Ta có: \({U_{AB}} = I.R = \frac{{168}}{{31}}.\frac{{24}}{7} = \frac{{576}}{{31}}V \to {U_{124}} = {U_{AB}} = \frac{{576}}{{31}}V\)
+ Lại có:\( {I_{12}} = {I_{124}} = \frac{{{U_{124}}}}{{{R_{124}}}} = \frac{{\frac{{576}}{{31}}}}{8} = \frac{{72}}{{31}}V\)
+ Dòng điện chạy qua ampe kế:
\( {I_A} = I - {I_1} = \frac{{168}}{{31}} - \frac{{48}}{{31}} = \frac{{120}}{{31}} \approx 3,87A\)
+ Hiệu điện thế hai đầu \( {R_1}:{U_1} = {U_{12}} = {I_{12}}{R_{12}} = \frac{{72}}{{31}}.2 = \frac{{144}}{{31}}V \to {I_1} = \frac{{{U_1}}}{{{R_1}}} = \frac{{\frac{{144}}{{31}}}}{3} = \frac{{48}}{{31}}A\)
.PNG)
.PNG)