Cho số phức z thỏa mãn: \(|z-2-2 i|=1\). Số phức z-i có môđun nhỏ nhất là:
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai\(\begin{array}{l} \text { Goi } z=x+y i, x, y \in \mathbb{R} \\ \text { Ta có: }|z-2-2 i|=1 \Leftrightarrow|(x-2)+(y-2) i|=1 \Leftrightarrow(x-2)^{2}+(y-2)^{2}=1 \end{array}\)
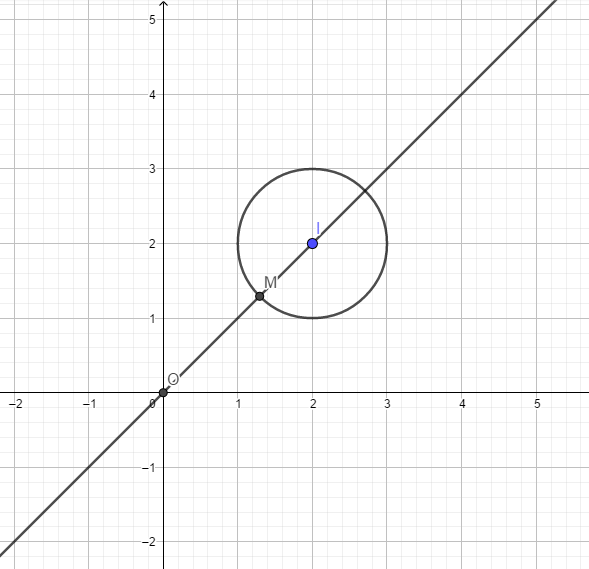
Tập hợp các điểm trong mặt phẳng Oxy biểu diễn của số phức z là đường tròn (C) tâm I(2; 2) và bán kính R =1.
\(|z-i|=\sqrt{x^{2}+(y-1)^{2}}=I M, \text { với } I(2 ; 2)\) là tâm đường tròn, M là điểm chạy trên đường tròn. Khoảng cách này ngắn nhất khi M là giao điểm của đường thẳng nối hai điểm \(N(0 ; 1) \in O y, I(2 ; 2)\) với đường tròn (C).
\(I M_{\min }=I N-R=\sqrt{5}-1\)
ADMICRO
YOMEDIA
ZUNIA9