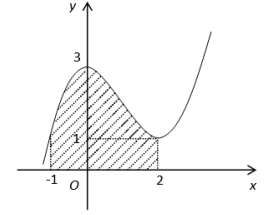
Diện tích hình phẳng giới hạn bởi đường cong: y = x2+1, tiếp tuyến với đường cong này tại M(2;5) và trục Oy là:
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiTa có: y' = 4
Phương trình tiếp tuyến với +1 tại M(2;5) là: y = 4(x - 2) + 5 = 4x - 3.
Ta có +1 = 4x−3 x = 2 khi đó diện tích hình phẳng cần tính là :
\(S = \int\limits_0^2 {\left| {{x^2} - 4x + 4} \right|dx = } \int\limits_0^2 {\left( {{x^2} - 4x + 4} \right)dx} = \left. {\left[ {\frac{{{x^3}}}{3} - 2{x^2} + 4x} \right]} \right|_0^2 = \frac{8}{3}\)
ADMICRO
YOMEDIA
ZUNIA9