Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f(x)=x-\sqrt{x}\) trên đoạn [ 0; 3] . Giá trị của biểu thức \(M+2 m\) gần với số nào nhất trong các số dưới đây ?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
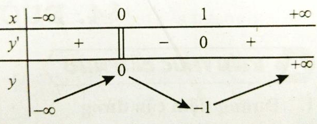
Báo sai\(\begin{array}{l} \text { Ta có } f^{\prime}(x)=1-\frac{1}{2 \sqrt{x}} ; f^{\prime}(x)=0 \Leftrightarrow 1-\frac{1}{2 \sqrt{x}}=0 \Leftrightarrow x=\frac{1}{4} \in(0 ; 3) \text { . } \\ f(0)=0, f\left(\frac{1}{4}\right)=-\frac{1}{4}, f(3)=3-\sqrt{3} \end{array}\)
\(\text { Suy ra, } M=3-\sqrt{3}, m=\frac{-1}{4} \Rightarrow M+2 m=\frac{5-2 \sqrt{3}}{2} \approx 0,7679491924 \ldots\)
ADMICRO
YOMEDIA
ZUNIA9
.jpg.png)
.jpg.png)
.jpg.png)











