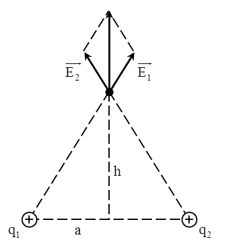
Hai điện tích \( q_1=q_2 (q > 0)\) đặt tại hai điểm A và B với AB = 2a. M là điểm nằm trên đường trung trực của AB và cách AB một đoạn h. Xác định h để cường độ điện trường tại M cực đại.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiCường độ điện trường tại điểm M là
\( \overrightarrow {{E_M}} = \overrightarrow {{E_1}} + \overrightarrow {{E_2}} \)
Trong đó \( \overrightarrow {{E_1}}; \overrightarrow {{E_2}}\) là cường độ điện trường do q1 và q2 gây ra tại M:
\( {E_1} = {E_2} = k\frac{{\left| {{q_1}} \right|}}{{{a^2} + {h^2}}}\)
Suy ra: Cường độ điện trường tổng hợp tại M:
\( {E_M} = {E_1}\cos \alpha = \frac{{2k\left| q \right|h}}{{{{({a^2} + {h^2})}^{1,5}}}}V/m\)
Áp dụng bất đẳng thức Cô-si, ta có:
\( {a^2} + {h^2} = \frac{{{a^2}}}{2} + \frac{{{a^2}}}{2} + {h^2} \ge 3\sqrt[3]{{\frac{{{a^4}{h^2}}}{2}}} \to {({a^2} + {h^2})^3} \ge \frac{{27}}{4}{a^4}{h^2} \to {({a^2} + {h^2})^{\frac{3}{2}}} \ge \frac{{3\sqrt 3 }}{2}{a^2}h\)
Vậy : \({E_M} \ge \frac{{2kqh}}{{\frac{{3\sqrt 3 }}{2}{a^2}h}} = \frac{{4kq}}{{3\sqrt 3 {a^2}}}\)
EM cực đại khi \( h = \frac{a}{{\sqrt 2 }} \to {E_M}_{(\max )} = \frac{{4kq}}{{3\sqrt 3 {a^2}}}\)