Khi điện tích trên tụ tăng từ 0 lên \( 0,5( \mu C )\) thì đồng thời cường độ dòng điện trong mạch dao động LC lí tưởng giảm từ \( 3\pi ( mA) \) xuống \( \frac{{3\sqrt 3 \pi }}{2}mA\) . Khoảng thời gian xảy ra sự biến thiên này là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có:
- Khi \( q = 0,i = 3\pi (mA) = {I_0}\)
⇒ Khi \( i = \frac{{3\sqrt 3 \pi }}{2}mA = \frac{{{I_0}\sqrt 3 }}{2}\)
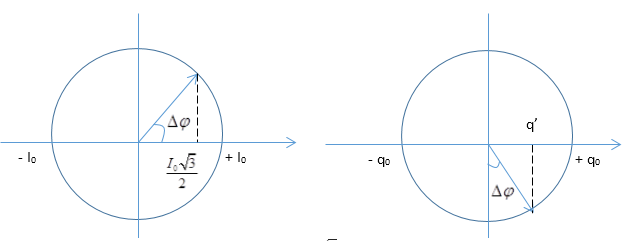
Vẽ vòng tròn lượng giác, ta được:
Từ vòng tròn lượng giác, ta có:
\( {\rm{cos\Delta }}\varphi = \frac{{\frac{{{I_0}\sqrt 3 }}{2}}}{{{I_0}}} = \frac{{\sqrt 3 }}{2} \to {\rm{\Delta }}\varphi = \frac{\pi }{6}\)
\(\begin{array}{*{20}{l}} { \to q' = {q_0}\sin {\rm{\Delta }}\varphi = {q_0}\sin \frac{\pi }{6} = \frac{{{q_0}}}{2} = 0,5\mu C \to {q_0} = 1\mu C}\\ { \to \omega = \frac{{{I_0}}}{{{q_0}}} = \frac{{3\pi {{.10}^{ - 3}}}}{{{{10}^{ - 6}}}} = 3\pi {{.10}^3}({\rm{r}}a{\rm{d}}/s)} \end{array}\)
Ta có:
\( {\rm{\Delta }}\varphi = \omega {\rm{\Delta }}t \to {\rm{\Delta }}t = \frac{{{\rm{\Delta }}\varphi }}{\omega } = \frac{{\frac{\pi }{6}}}{{3\pi {{.10}^3}}} = \frac{1}{{18}}{.10^{ - 3}} = \frac{1}{{18}}ms\)
Đáp án cần chọn là: D