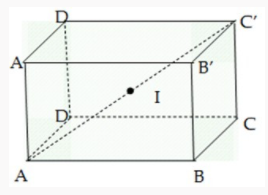
Một hình hộp chữ nhật nội tiếp mặt cầu có ba kích thước là a, b, c. Tìm bán kính r của mặt cầu bằng?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có tâm của mặt cầu ngoại tiếp hình hộp chữ nhật trùng với tâm đối xứng của hình hộp. Như hình lập phương ABCD.A’B’C’D’ có tâm là I, là trung điểm của AC’, bán kính\( r = \frac{{AC'}}{2}\)
Tam giác A'C'A vuông tại A'\( \Rightarrow AC' = \sqrt {A{A^{\prime 2}} + A'{C^2}} = \sqrt {{c^2} + A'{C^{\prime 2}}} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)\)
Mặt khác tam giác A'D'C' vuông tại D'\( \Rightarrow A'C' = \sqrt {A'{D^{\prime 2}} + D'{C^{\prime 2}}} = \sqrt {{a^2} + {b^2}} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 2 \right)\)
Từ (1) và (2) ta có \( r = \frac{1}{2}.\sqrt {{a^2} + {b^2} + {c^2}} \)
Câu hỏi liên quan
-
Một mặt cầu có diện tích \(16{\rm{\pi }}\) thì bán kính mặt cầu bằng
-
Cho hình chóp tam giác S.ABC có \( \widehat {SAC} = \widehat {SBC} = {90^0}\) Khi đó tâm mặt cầu ngoại tiếp hình chóp nằm trên đường thẳng nào?
-
Cho hình chóp \(S.ABC\) có \(SA\bot \left( ABC \right)\), \(AC=b\), \(AB=c\), \(\widehat{BAC}=\alpha \). Gọi \({B}'\), \({C}'\) lần lượt là hình chiếu vuông góc của \(A\) lên \(SB\), \(SC\). Tính bán kính mặt cầu ngoại tiếp hình chóp \(A.BC{C}'{B}'\) theo \(b\), \(c\), \(\alpha .\)
-
Người ta cần đổ một ống thoát nước hình trụ bằng bê tông với chiều cao 100cm, độ dày của thành ống là 10cm và đường kính của ống là 50cm. Lượng bê tông cần phải đổ là:
-
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với mặt phẳng (ABC) và \(AB = 2, AC = 4,SA = \sqrt5\)Mặt cầu đi qua các đỉnh của hình chóp (S.ABC ) có bán kính là
-
Cho mặt cầu \(\left( S \right)\) Có tâm \(I\), bán kính \(R=5\). Một đường thằng \(\Delta \) cắt \(\left( S \right)\) tại \(2\) điểm \(M\), \(N\) phân biệt nhưng không đi qua \(I\). Đặt \(MN=2m\). Với giá trị nào của m thì diện tích tam giác \(IMN\) lớn nhất?
-
Trong không gian Oxyz, cho mặt cầu \(\left( S \right): {x^2} + {y^2} + {z^2} – 2x + 4y – 4z – 16 = 0\) có tâm \(I\left( {a;b;c} \right)\) và bán kính r. Khi đó, giá trị của biểu thức L = a + b + c + r bằng
-
Trong không gian với hệ tọa độ Oxyz, \(A(-3 ; 4 ; 2), B(-5 ; 6 ; 2), C(-10 ; 17 ;-7)\). Viết phương trình mặt cầu tâm C bán kính AB .
-
Trong không gian, cho bốn mặt cầu có bán kính lần lượt là 2,3,3,2(đơn vị độ dài) đôi một tiếp xúc ngoài với nhau. Mặt cầu nhỏ nhất tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng
-
Viết phương trình mặt cầu tiếp xúc với cả ba mặt phẳng tọa độ và đi qua điểm M(2;1;1).
-
Trong không gian Oxyz, cho ba điểm \(A\left( {2;0;0} \right), B\left( {0; – 3;0} \right)\) và \(C\left( {0;0;6} \right)\). Bán kính mặt cầu ngoại tiếp hình chóp OABC là:
-
Một nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng một hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết SO=h;OB=R;OH=x0<x<h. Tìm thể tích lớn nhất của hình trụ.
-
Cho mặt cầu \(\left( S \right)\) có tâm \(I\left( {1;2;3} \right)\) và diện tích bằng \(32\pi .\) Phương trình của \(\left( S \right)\) là
-
Viết phương trình mặt cầu (S) có tâm A(1;0;1) và cắt mặt phẳng (P):x−y+z−1=0 với thiết diện là hình tròn có đường kính bằng 2.
-
Người ta muốn xây một chiếc bể chứa nước có hình dạng là một khối hộp chữ nhật không nắp có thể tích bằng 500/3 m3. Biết đáy hồ là một hình chữ nhật có chiều dài gấp đôi chiều rộng và giá thuê thợ xây là 100.000 đồng /m2. Tìm kích thước của hồ để chi phí thuê nhân công ít nhất. Khi đó chi phí thuê nhân công là
-
Trong không gian với hệ trục tọa độ Oxyz, mặt cầu \(\left( S \right):{\left( {x + 2} \right)^2} + {\left( {y – 1} \right)^2} + {z^2} = 4\) có tâm I và bán kính R lần lượt là
-
Cho hình chóp \(S.ABC\)có \(SA\)vuông góc với mặt phẳng \(\left( ABC \right),\,\,SA=a,\,\,AB=a\),\(AC=2a,\) \(\widehat{BAC}={{60}^{0}}.\) Tính diện tích hình cầu ngoại tiếp hình chóp \(S.ABC\).
-
Trong các phương trình sau, phương trình nào không phải là phương trình mặt cầu?
-
Cho mặt cầu \(\left( S \right)\) tâm O, bán kính R và mặt phẳng \(\left( P \right)\) có khoảng cách đến O bằng R. Một điểm M tùy ý thuộc (S). Đường thẳng OM cắt \(\left( P \right)\) tại N. Hình chiếu của O trên \(\left( P \right)\) là I. Mệnh đề nào sau đây là đúng?
-
Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left( {5;1; – 1} \right), B\left( {14; – 3;3} \right)\) và đường thẳng \(\Delta \) có vectơ chỉ phương \(\vec u = \left( {1;2;2} \right)\). Gọi C, D lần lượt là hình chiếu của A và B lên \(\Delta \). Mặt cầu đi qua hai điểm C, D có diện tích nhỏ nhất là
