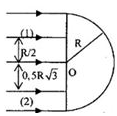
Một miếng gỗ mỏng hình tròn, bán kính 4cm. Người ta cắm thẳng góc một chiếc đinh qua tâm O của miếng gỗ nổi trong chậu nước. Thành chậu thẳng đứng và rìa miếng gỗ cách thành chậu 10cm. Nước có chiết suất n = 1,33. Gọi chiều dài phần đinh nằm trong nước là OA = 6cm. Tìm chiều dài lớn nhất của OA sao cho dù để mắt ở đâu cũng không thấy đầu A của đinh.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiMột miếng gỗ mỏng hình tròn, bán kính; R = 4cm
Điều kiện để mắt ở đâu cũng không thấy đầu A của đinh là: Tia sáng từ A phát ra truyền tới mặt nước thì không cho tia khúc xạ ra ngoài không khí.
.PNG)
Ta thấy góc tới i của tia sáng phát ra từ A đến mặt nước tăng dần khi vị trí tới di chuyển từ điểm I của mép miếng gỗ ra xa tâm O. Để không có bất kỳ tia khúc xạ nào lọt ra ngoài không khí thì tia tới AI phải có góc tới thỏa mãn điều kiện: \( i \ge {i_{gh}}\: \Leftrightarrow \sin i \ge \sin {i_{gh}}\: = \frac{1}{n}\)
Ta có:
\(\begin{array}{*{20}{l}} {\sin i = \sin \widehat {OAI} = \frac{{OI}}{{AI}} = \frac{R}{{\sqrt {O{A^2} + {R^2}} }} \ge \frac{1}{n}}\\ { \Leftrightarrow \sqrt {O{A^2} + {R^2}} \le R.n \Leftrightarrow O{A^2} + {R^2} \le {R^2}.{n^2}}\\ { \Leftrightarrow OA \le R\sqrt {{n^2} - 1} = 4.\sqrt {{{1,33}^2} - 1} = 3,51cm}\\ { \Rightarrow O{A_{\max }} = 3,51cm} \end{array}\)
Câu hỏi liên quan
-
Khi ánh sáng truyền từ môi trường chiết suất lớn sang môi trường có chiết suất nhỏ hơn thì
-
Khi chiếu tia sáng từ môi trường trong suốt có chiết suốt n= 2 ra ngoài không khí thì góc giới hạn phản xạ toàn phần bằng:
-
Hiện tượng phản xạ toàn phần là hiện tượng
-
Điều kiện cần để xảy ra hiện tượng phản xạ toàn phần nào sau đây là sai?
-
Hiện tượng nào sau đây không được giải thích bằng hiện tượng phản xạ toàn phần?
-
Trong các câu sau đây, câu nào sai? Khi một tia sáng đi từ môi trường có chiết suất n1, tới mặt phân cách với một môi trường có chiết suất n2 < n1 thì
-
Sợi quang trong cáp quang ứng dụng hiện tượng
-
Trong Y khoa có sử dụng thuật ngữ "nội soi", vậy người ta đã ứng dụng hiện tượng nào sau đây để chế tạo dụng cụ khi nội soi?
-
Một chùm tia sáng hẹp SI truyền trong mặt phẳng tiết diện vuông góc của một khối trong suốt như hình vẽ. Tia sáng phản xạ toàn phần ở mặt AC. Trong điều kiện đó, chiết n của khối trong suốt có giá trị như thế nào?
-
Một sợi quang hình trụ, lõi có chiết suất nl = 1,5, phần võ bọc có chiết suất nv=√2 . Chùm tia tới hội tụ ở mặt trước của sợi với góc 2α như hình vẽ. Tìm điều kiện α để các tia sáng của chùm sáng truyền được trong ống
-
Một khối bán trụ trong suốt có chiết suất (\(n = 1,41 \approx \sqrt2\) ). Một chùm tia sáng hẹp nằm trong mặt phẳng của tiết diện vuông góc, chiếu tới khối bán trụ như hình vẽ. Xác định góc khúc xạ ló ra ngoài không khí. Biết α = 600
-
Một tia sáng đi từ một chất lỏng trong suốt có chiết suất n sang không khí, nếu α=600 thì β=300 như hình. Góc α lớn nhất mà tia sáng không thể ló sang môi trường không khí phía trên là?
-
Một đĩa tròn mỏng bằng gỗ, bán kính R = 5cm nổi trên mặt nước. Ở tâm đĩa có gắn một cây kim, thẳng đứng, chìm trong nước có chiết suất n = 4/3. Dù đặt mắt ở đâu cũng không thấy cây kim. Chiều dài tối đa của cây kim là:
-
Tia sáng đi từ không khí vào chất lỏng trong suốt với góc tới i = 450 thì góc khúc xạ r = 300. Khi tia sáng đi từ chất lỏng ra không khí, để xảy ra phản xạ toàn phần thì góc tới i phải thỏa
-
Một tấm thủy tinh mỏng, trong suốt, chiết suất n1 = 1,6 có tiết diện là hình chữ nhật ABCD (AB rất lớn so với AD) mặt đáy AB tiếp xúc với một chất lỏng có chiết suất \(n_2=\sqrt2\). Chiếu tia sáng SI nằm trong mặt phẳng ABCD tới mặt AD sao cho tia tới nằm phía trên pháp tuyến ở điểm tới và tia khúc xạ trong thủy tinh gặp đáy AB ở điểm K. Giá trị lớn nhất của góc tới i để có phản xạ toàn phần tại K.
-
Cho một khối thuỷ tinh hình hộp chữ nhật có tiết diện thẳng ABCD đặt trong không khí. Để mọi tia sáng tới mặt có cạnh AB đều phản xạ toàn phần ở mặt có cạnh BC thì chiết suất n của thuỷ tinh có giá trị nhỏ nhất là
-
Điều kiện để xảy ra hiện tượng phản xạ toàn phần là góc tới i
-
Chiếu một tia sáng đơn sắc từ trong nước tới mặt phân cách với không khí. Biết chiết suất của nước và của không khí đối với ánh sáng đơn sắc này lần lượt là 1,333 và 1. Góc giới hạn phản xạ toàn phần ở mặt phân cách giữa nước và không khí đối với ánh sáng đơn sắc này là
-
Một bể chứa nước có thành cao 80cm, đáy phẳng dài 120mm. Độ cao mực nước trong bể là 60cm và có chiết suất là 4/3. Ánh nắng chiếu theo phương nghiêng 300 so với mặt nước trong bể. Độ dài bóng đen tạo thành ở dưới đáy bể?
-
Một khối thuỷ tinh hình bán cầu tâm O bán kính 20cm, chiết suất n = 1,414. Chiếu chùm tia sáng song song vào toàn bộ mặt phẳng của hình bán cầu theo phương vuông góc với mặt phẳng đó. Bán kính đường đi của chùm tia sáng tới bán cầu mà cho chùm tia ló ra khỏi mặt cong của nó là?
