Một vật dao động điều hòa với chu kì T và biên độ A. Hãy tính khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ: \({x_1} = \frac{A}{2} \to {x_2} = - \frac{{A\sqrt 3 }}{2}\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐi từ \({x_1} = \frac{A}{2}\) theo chiều âm đến\(- \frac{{A\sqrt 3 }}{2}\) theo chiều âm.
Đi từ \({x_1} = \frac{A}{2}\) theo chiều âm đến \(- \frac{{A\sqrt 3 }}{2}\) theo chiều dương.
Đi từ \({x_1} = \frac{A}{2}\) theo chiều dương đến \(- \frac{{A\sqrt 3 }}{2}\)theo chiều âm.
Đi từ \({x_1} = \frac{A}{2}\) theo chiều dương đến \(- \frac{{A\sqrt 3 }}{2}\)theo chiều dương.
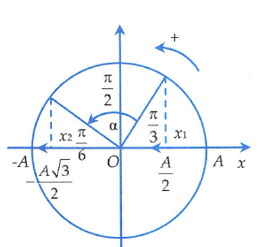
Tuy nhiên trong 4 trường hợp trên thì thời gian ngắn nhất ứng với trường hợp đi từ \({x_1} = \frac{A}{2}\) theo chiều âm đến \(- \frac{{A\sqrt 3 }}{2}\) theo chiều âm. Chúng ta xem đường tròn hình bên để hiểu rõ hơn.
Dựa vào đường tròn, ta có \(\alpha = \frac{\pi }{2}\) nên thời gian là \(t = \frac{T}{4}\) .
.PNG)











