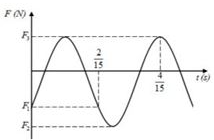
Một con lắc lò xo gồm một vật nhỏ có khối lượng m=200g và lò xo có độ cứng k, đang dao động điều hòa theo phương thẳng đứng. Chọn gốc tọa độ ở vị trí cân bằng, chiều dương hướng xuống dưới. Đồ thị biểu diễn sự phụ thuộc của lực đàn hồi theo thời gian được cho như hình vẽ. Biết \(F_1+ 3F_2 + 6F_ 3= 0 \). Lấy \(g = 10 m/s^2\). Tỉ số thời gian lò xo giãn với thời gian lò xo nén trong một chu kì gần giá trị nào nhất sau đây?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTừ đồ thị ta thấy:
Lực đàn hồi tại thời điểm ban đầu: \(F=F_1=−k(Δl_0+x)\)
Lực đàn hồi tại vị trí biên dương: \(F=F_2=−k(Δl_0+A)\)
Lực đàn hồi tại vị trí biên âm: \(F=F_3=−k(Δl_0–A)\)
Gọi Δt là thời gian từ t=0 đến \( t = \frac{2}{{15}}s\)
Ta có: \( T + \frac{{{\rm{\Delta }}t}}{2} = 2{\rm{\Delta }}t \Rightarrow {\rm{\Delta }}t = \frac{{2T}}{3} \Rightarrow x = \frac{A}{2}\)
Theo đề bài:
\( {F_1} + 3{F_2} + 6{F_3} = 0 \Leftrightarrow k\left( {{\rm{\Delta }}{l_0} + x} \right) + 3k\left( {{\rm{\Delta }}{l_0} + A} \right) + 6k\left( {{\rm{\Delta }}{l_0} - A} \right) = 0 \Rightarrow {\rm{\Delta }}{l_0} = 0,25A\)
=> Thời gian lo xo nén là :
\( {t_n} = \frac{{2\alpha }}{{360}}T = \frac{{151}}{{360}}T = 0,42T \Rightarrow {t_g} = T - {t_n} = 0,58T\)
Tỉ số thời gian giãn và nén trong một chu kì:
\( \frac{{{t_g}}}{{{t_n}}} = \frac{{0,58}}{{0,42}} = 1,381\)
Câu hỏi liên quan
-
Vật dao động điều hòa với phương trình\(x = 5cos\left( {6\pi t + \frac{\pi }{6}} \right)cm\). Xác định số lần vật đi qua vị trí x=2,5cm theo chiều âm kể từ thời điểm t = 2s đến t = 3,25s ?
-
Một vật tham gia đồng thời hai dao động điều hoà cùng phương, cùng tần số có phương trình \( {x_1} = 3\cos (4\pi t + \frac{\pi }{6})cm\) và \( {x_2} = 7\cos (4\pi t + \frac{{13\pi }}{6})cm\). Dao động tổng hợp có phương trình là
-
Hai dao động điều hòa cùng phương, cùng chu kì có phương trình lần lượt là \( {x_1} = 4c{\rm{os}}(10\pi {\rm{t}} + \frac{\pi }{3})(cm);{x_2} = 2c{\rm{os}}(10\pi {\rm{t}} + \pi )(cm)\). Tìm phương trình của dao động tổng hợp.
-
Một vật tham gia vào hai dao động điều hòa có cùng tần số thì
-
Một vật tham gia đồng thời hai dao động điều hoà cùng phương, có phương trình lần lượt là x1 = 6sin(πt + φ1) cm và x2 = 8cos(πt + π/3) cm. Khi biên độ dao động tổng hợp có giá trị A = 14 cm thì pha ban đầu của dao động thứ nhất là
-
Một vật tham gia đồng thời hai dao động điều hòa, cùng phương, cùng tần số, cùng biên độ là A và lệch pha nhau π/2. Biên độ dao động tổng hợp của hai dao động trên bằng
-
Cho ba dao động điều hòa cùng phương cùng tần số có phương trình lần lượt là x1 = 2acosωt (cm); x2 = A2cos(ωt + φ2) (cm) và x3 = acos(ωt + π) (cm). Gọi x12 = x1 + x2 và x23 = x2 + x3. Biết đồ thị sự phụ thuộc x12 và x23 theo thời gian như hình vẽ. Tính φ2.
.PNG)
-
Hai chất điểm M và N dao động điều hòa cùng chu kì T = 4s dọc theo hai đường thẳng song song kề nhau và song song với trục Ox. Vị trí cân bằng của M và N đều ở trên cùng một đường thẳng qua gốc tọa độ và vuông góc với Ox. Trong quá trình dao động, khoảng cách lớn nhất giữa M và N theo phương Ox là 10 cm. Tại thời điểm t1 hai vật đi ngang qua nhau, hỏi sau thời gian ngắn nhất là bao nhiêu kể từ thời điểm t1 khoảng cách giữa chúng bằng 5√2 cm
-
Trong dao động điều hoà, vận tốc biếu đổi điều hòa A. B. C. D.
-
Hai chất điểm dao động điều hòa với chu kỳ T, lệch pha nhau \(\frac{\pi }{3}\) với biên độ lần lượt là A và 2A, trên hai trục tọa độ song song cùng chiều, gốc tọa đó nằm trên đường vuông góc chung. Khoảng thời gian nhỏ nhất giữa hai lần chúng ngang nhau là:
-
Một vật dao động với biên độ A, chu kỳ T. Tính tốc độ trung bình lớn nhất vật có thể đạt được trong \(\frac{2T}{3}\)?
-
Một vật dao động điều hòa trong thời gian 20 giây vật thực hiện được 80 dao động toàn phần. Tần số dao động của vật là:
-
Trong các phương trình sau phương trình nào không biểu thị cho dao động điều hòa?
-
Một vật có khối lượng 0,5 kg thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số góc 4π rad/s, x1 = A1cos(ωt + π/6) cm và x2 = 4sin(ωt - π/3) cm. Biết hợp lực tác dụng lên vật có độ lớn cực đại là 2,4 N. Biên độ A1 có giá trị:
-
Một vật thực hiện đồng thời hai dao động điều hoà cùng phương, có các phương trình lần lượt là \( {x_1} = a\cos \omega t(cm)\) và \( {x_2} = 2a\cos (\omega t + \frac{2\pi }{3})(cm)\) . Phương trình dao động tổng hợp là
-
Một vật dao động điều hòa với phương trình chuyển động \(x = 2cos\left( {4\pi t - \frac{\pi }{2}} \right)cm\). Thời điểm để vật đi qua li độ \(x = \sqrt 3 cm\)theo chiều âm lần đầu tiên kể từ thời điểm t = 2s là:
-
Xét dao động tổng hợp của hai dao động thành phần có cùng tần số, biên độ dao động tổng hợp không phụ thuộc vào yếu tố nào sau đây?
-
Một chất điểm dao động điều hòa trên trục Ox. Tốc độ trung bình của chất điểm tương ứng với khoảng thời gian thế năng không vượt quá ba lần động năng trong một nửa chu kỳ là \(300\sqrt 3 \) cm/s. Tốc độ cực đại của dao động là
-
Một vật dao động điều hòa với chu kì T và biên độ A. Hãy tính khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ: \({x_1} = \frac{A}{2} \to {x_2} = - \frac{{A\sqrt 3 }}{2}\)
-
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số có dạng \(x_1 = A_1cos 10t ; x_2 = A_2cos (10t + \varphi _2 )\). Biết phương trình dao động tổng hợp là \(x = A_1\sqrt 3 cos ( 10t + \varphi)\), trong đó \( {\varphi _2} - \varphi = \frac{\pi }{6}\) Xác định tỉ số \( \frac{\varphi }{{{\varphi _2}}}\)
