Tìm tập hợp tất cả giá trị thực của tham số m để đồ thị hàm số y = x⁴ - 2(m + 1) x² + m có ba điểm cực trị A, B, C sao cho OA = BC;trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTXĐ: \(D=\mathbb{R}\)
\(\begin{array}{l} y' = 4{x^3} - 4\left( {m + 1} \right)x = 4x\left( {{x^2} - m - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} x = 0\\ {x^2} = m + 1\,\,\,\,\,\,(1) \end{array} \right. \end{array}\)
Đồ thị hàm số có 3 điểm cực trị khi vào chỉ khi (1) có hai nghiệm phân biệt khác 0\(\Leftrightarrow m>-1\,\,\,\,\,(2)\).
Khi đó:
\(\begin{array}{l} A(0;m),B\left( { - \sqrt {m + 1} ; - {m^2} - m - 1} \right),C\left( {\sqrt {m + 1} ; - {m^2} - m - 1} \right)\\ O{A^2} = {m^2},B{C^2} = 4(m + 1)\\ OA = BC \Leftrightarrow O{A^2} = B{C^2}\\ \Leftrightarrow {m^2} = 4\left( {m + 1} \right)\\ \Leftrightarrow \left[ \begin{array}{l} m = 2 - 2\sqrt 2\,\,\, \rm{thỏa\,(2)} \\ m = 2 + 2\sqrt 2 \,\,\,\rm{thỏa\,(2)} \end{array} \right. \end{array}\)
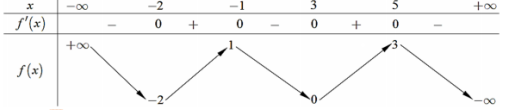
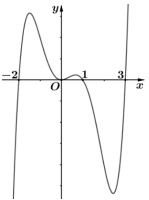
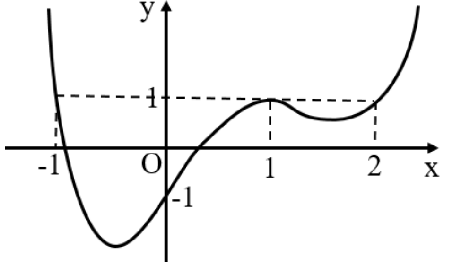
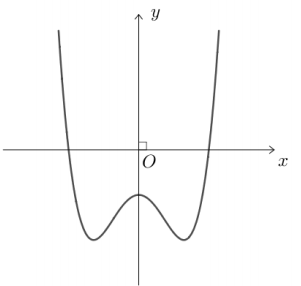
.png)
.jpg.png)
.png)











