Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình \(3(\sqrt{1+x}+\sqrt{3-x})-2 \sqrt{(1+x)(3-x)} \geq m\) nghiệm đúng với mọi \(x \in[-1 ; 3] ?\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(t=\sqrt{1+x}+\sqrt{3-x} \Rightarrow t^{2}=4+2 \sqrt{(1+x)(3-x)} \Leftrightarrow 2 \sqrt{(1+x)(3-x)}=t^{2}-4 \)
Với \(x \in[-1 ; 3]=>t \in[2 ; 2 \sqrt{2}\)
Thay vào bất phương trình ta được \(m \leq-t^{2}+3 t+4\)
Xét hàm số \(f(t)=-t^{2}+3 t+4 ; f^{\prime}(t)=-2 t+3 ; f^{\prime}(t)=0 \Leftrightarrow t=\frac{3}{2}<2\)
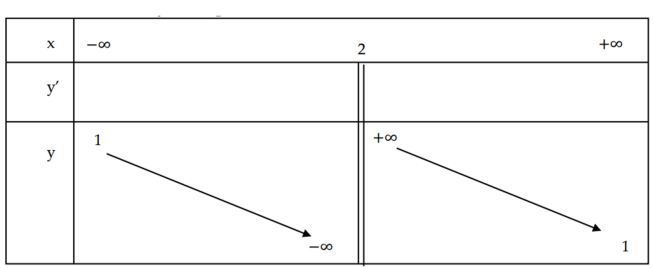
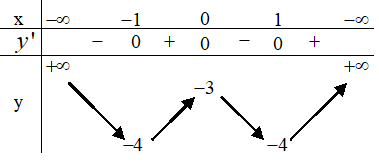
Bảng biến thiên
Từ bảng biến thiên ta có \(m \leq 6 \sqrt{2}-4\) thỏa đề bài
Câu hỏi liên quan
-
Đồ thị sau đây là của hàm số nào:
-
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
.png)
-
Đồ thị sau đây là của hàm số nào?
-
Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
Phương trình f(x)-2=0 có tất cả bao nhiêu nghiệm?
-
Đồ thị hình bên là của hàm số nào? Chọn một khẳng định ĐÚNG
-
Tìm tất cả các giá trị thực của tham số m sao cho phương trình \(2 \sqrt{x+1}=x+m\) có nghiệm thực?
-
Bảng biến thiên sau đây là của hàm số nào ?
-
Cho phương trình x3 - 3x2 + 1 - m = 0 (1). Điều kiện của tham số m để (1) có ba nghiệm phân biệt thỏa x1 < 1 < x2 < x3 khi
-
Cho hàm số y=f(x) liên tục trên đoạn [-2;2] và có đồ thị là đường cong như trong hình vẽ bên.
Hỏi phương trình \(|f(x)-1|=2\) có mấy nghiệm phân biệt trên [-2;2]? -
Số giao điểm của trục hoành và đồ thị hàm số y = - x4 + 2x2 + 3 là:
-
Tọa độ giao điểm có hoành độ nhỏ hơn 1 của đường (C): \(y = \frac{{3x - 1}}{{x - 1}}\) và đường thẳng (d): y = x + 1 là:
-
Cho hàm số y = ax4 + bx2 + c có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
-
Cho hàm số y = x3-3x2-m-1 có đồ thị (C). Giá trị của tham số m để đồ thị (C) cắt trục hoành tại ba điểm phân biệt lập thành cấp số cộng là
-
Biết đồ thị hàm số \( y = \frac{{2x - 1}}{{x + 3}}\) cắt trục Ox,Oy lần lượt tại hai điểm phân biệt A, B. Tính diện tích S của tam giác OAB
-
Bảng biến thiên dưới đây là bảng biến thiên của hàm số nào trong các hàm số được liệt kê ở bốn phương án A, B, C, D?
-
Cho hàm của hàm số f(x) đồng biến trên tập số thực R, mệnh đề nào sau đây là đúng ?
-
Bảng biến thiên sau đây là của hàm số nào?
-
Bảng biến thiên sau đây là của hàm số nào?
-
Đường cong hình bên là đồ thị của một hàm số nào trong bốn hàm số dưới đây
.png)
-
Cho hàm số \(y=\frac{2x-1}{x-1}\)có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số \(y=\frac{|2x-1|}{x-1}\)
.png)
