Tính diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = x2 , y = 4x - 4 và y = -4x - 4
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai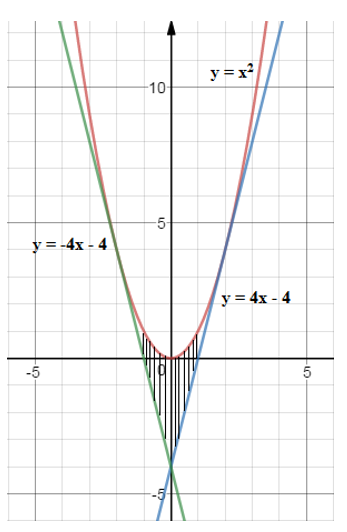
Ta thấy đường thẳng y = -4x - 4 và đường thẳng y = 4x - 4 lần lượt là hai tiếp tuyến của đồ thị hàm số y = x2 tại các tiếp điểm có hoành độ x = - 2 và x = 2.
Do tính đối xứng qua Oy của parabol y = x2 nên diện tích hình phẳng cần tìm bằng 2 lần diện tích tam giác cạnh OMT2 và bằng:
\(2\mathop \smallint \nolimits_0^2 \left[ {{x^2} - \left( {4x - 4} \right)} \right]dx\; = \;2\mathop \smallint \nolimits_0^2 {\left( {x - 2} \right)^2}dx\; = \;2\frac{{{{\left( {x - 2} \right)}^3}}}{3}\;\left| {\left| {\begin{array}{*{20}{c}}
2\\
{}\\
0
\end{array}\; = \;\frac{{16}}{3}} \right.} \right.\)











