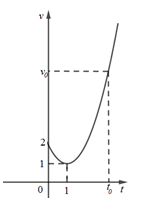
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số trục hoành, trục tung và đường thẳng
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
ZUNIA9