Trong không gian, cho bốn mặt cầu có bán kính lần lượt là 2,3,3,2(đơn vị độ dài) đôi một tiếp xúc ngoài với nhau. Mặt cầu nhỏ nhất tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai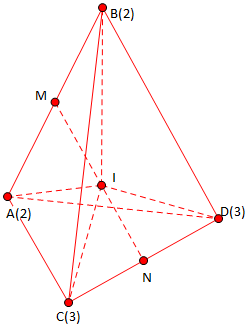
Gọi A, B là tâm mặt cầu bán kính bằng 2; C, Dlà tâm mặt cầu bán kính bằng 3; I là tâm mặt cầu bán kính x tiếp xúc ngoài với 4 mặt cầu tâm A,B,C,D nói trên.
Dễ thấy A,B,C,D không đồng phẳng.
Gọi \(M,\,N\) lần lượt là trung điểm của AB và CD.
Mặt cầu \(\left( I \right)\) tiếp xúc ngoài với 4 mặt cầu tâm A,B,C,D nên \(IA = IB = x + 2,\,\,IC = ID = x + 3\).
Gọi \(\left( P \right), \left( Q \right)\) lần lượt là các mặt phẳng trung trực đoạn AB và CD.
Ta có \(M \in \left( P \right); N \in \left( Q \right)\).
\(\left\{ \begin{array}{l}IA = IB \Rightarrow I \in \left( P \right)\\IC = ID \Rightarrow I \in \left( Q \right)\end{array} \right. \Rightarrow I \in \left( P \right) \cap \left( Q \right)\,\,\,\left( 1 \right)\).
Tứ diện ABCD có DA = DB = CA = CB = 5 nên \(\Delta CAB = \Delta DAB \Rightarrow NA = NB$ hay \(N \in \left( P \right)\).
Tương tự chứng minh được \(M \in \left( Q \right)\).
suy ra \(MN = \left( P \right) \cap \left( Q \right)\) và MN là đường vuông góc chung của AB và CD. (2).
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(I \in MN\)
Tam giác IAM có \(IM = \sqrt {I{A^2} – A{M^2}} = \sqrt {{{\left( {x + 2} \right)}^2} – 4} \)
Tam giác CIN có \(IN = \sqrt {I{C^2} – C{N^2}} = \sqrt {{{\left( {x + 3} \right)}^2} – 9} \)
Tam giác ABN có \(NM = \sqrt {N{A^2} – A{M^2}} = \sqrt {12} \)
Suy ra \(\sqrt {{{\left( {x + 3} \right)}^2} – 9} + \sqrt {{{\left( {x + 2} \right)}^2} – 4} = \sqrt {12} \Leftrightarrow \sqrt {{x^2} + 6x} + \sqrt {{x^2} + 4x} = \sqrt {12} \)
\( \Leftrightarrow \sqrt {{x^2} + 6x} = \sqrt {12} – \sqrt {{x^2} + 4x} \)
\( \Rightarrow {x^2} + 6x = 12 + {x^2} + 4x – 4\sqrt {3{x^2} + 12x} \Leftrightarrow 2\sqrt {3{x^2} + 12x} = 6 – x\)
\( \Leftrightarrow \left\{ \begin{array}{l}x \le 6\\12{x^2} + 48x = 36 – 12x + {x^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 6\\11{x^2} + 60x – 36 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 6\\\left[ \begin{array}{l}x = \frac{6}{{11}}\\x = – 6\end{array} \right.\end{array} \right.\).
Vì bán kính không âm nên: \(x = \frac{6}{{11}}\).











