Với giá trị nào của m, phương trình \(4^{x}-2^{x}+m=0\) có nghiệm?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐặt \(t=2^{x}, t>0\)
Phương trình trở thành \(: t^{2}-t+m=0(*)\)
Để phương trình ban đầu có nghiệm thì (*) phải có ít nhất 1 nghiệm dương.
Thông thường để định điều kiện cho (*) ta phải hợp các trường hợp: phương trình có 2 ngiệm dương, phương trình có nghiệm kép dương và phương trình có 2 nghiệm trái dấu.
\(\left[\begin{array}{l} \Delta>0 ; S>0 ; P>0 \\ \Delta=0 ; S>0 \\ P<0 \end{array}\right.\)
mà t>0 nên ta xét
\((*)\Leftrightarrow m=t-t^{2}=f(t)(1)\)
Ta có bẳng biến thiên f(t):
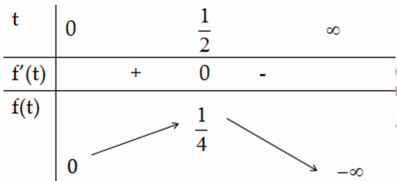
Số nghiệm của phương trình (*) là giao điểm của đường thẳng y = m với đồ thị hàm f(t)
Dựa vào bảng biến thiên suy ra (*) có ít nhất 1 ngiệm dương khi và chỉ khi \(0 \leq m<\frac{1}{4}\)











