Trắc nghiệm Vectơ trong không gian Toán Lớp 11
-
Câu 1:
Cho hình hộp \(A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}\) . Gọi I và K lần lượt là tâm của hình bình hành \(A B B^{\prime} A^{\prime}\) và \(B C C^{\prime} B\) . Khẳng định nào sau đây sai?
-
Câu 2:
Cho hình hộp ABCD A'B'C'D' . có tâm O . Gọi I là tâm hình bình hành ABCD . Đặt \(\overrightarrow{A C^{\prime}}=\vec{u}, \overrightarrow{C A^{\prime}}=\vec{v}, \overrightarrow{B D^{\prime}}=\vec{x}, \overrightarrow {D B^{\prime}}=\vec{y}\) . Khẳng định nào sau đây đúng?
-
Câu 3:
Cho tứ diện ABCD . Gọi M và P lần lượt là trung điểm của AB và CD . Đặt \(\overrightarrow{A B}=\vec{b},\overrightarrow{A C}=\vec{c}, \overrightarrow{A D}=\vec{d}\). Khẳng định nào sau đây đúng?
-
Câu 4:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Đặt \(\overrightarrow{S A}=\vec{a} ; \overrightarrow{S B}=\vec{b} ; \overrightarrow{S C}=\vec{c},\overrightarrow{S D}=\vec{d}\). Khẳng định nào sau đây đúng?
-
Câu 5:
Trong không gian cho điểm O và bốn điểm A , B , C , D không thẳng hàng. Điều kiện cần và đủ để A , B , C , D tạo thành hình bình hành là
-
Câu 6:
Cho hình lăng trụ \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\), M là trung điểm của BB' . Đặt \(\overrightarrow{C A}=\vec{a}, \overrightarrow{C B}=\vec{b}, \overrightarrow{A A^{\prime}}=\vec{c}\). Khẳng định nào sau đây đúng?
-
Câu 7:
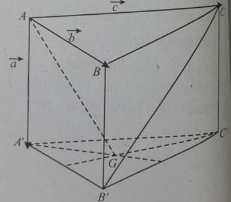
Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt \(\overrightarrow {AA'} \; = \;\vec a,\;\overrightarrow {AB} \; = \;\vec b,\;\overrightarrow {AC} \; = \;\vec c\)
Vecto \(\overrightarrow {AG} \) bằng:
-
Câu 8:
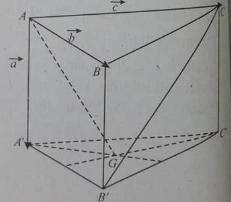
Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c \)
Vecto \(\overrightarrow {B'C} \) bằng:
-
Câu 9:
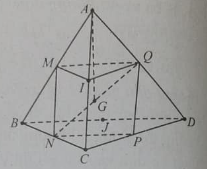
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
\(\overrightarrow {AB} \; + \;\overrightarrow {AC} \; + \;\overrightarrow {AD} \) bằng:
-
Câu 10:
Ba vecto \(\vec a,\;\vec b,\;\vec c\) không đồng phẳng nếu?
-
Câu 11:
Cho ba vecto \(\vec a,\;\vec b,\;\vec c\). Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng.
-
Câu 12:
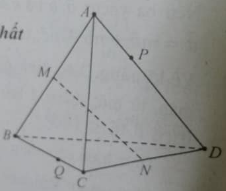
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Lấy hai điểm P và Q lần lượt thuộc AD và BC sao cho \(\overrightarrow {PA} \; = \;m\overrightarrow {PD} \) và \(\overrightarrow {QB} \; = \;m\overrightarrow {QC} \), với m khác 1. Vecto \(\overrightarrow {MP}\) bằng:
-
Câu 13:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
Từ A hạ AH ⊥ SM. Khi đó góc giữa hai vecto \(\overrightarrow {SA} \) và \(\overrightarrow {AH} \) bằng:
.png)
-
Câu 14:
Cho hình chóp S.ABCD, với O là giao điểm của AC và BD. Mệnh đề nào sau đây là đúng?
-
Câu 15:
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm của tứ diện ABCD trong trường hợp
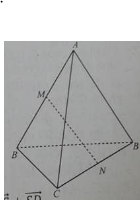
-
Câu 16:
Điều kiện cần và đủ để ba vecto \(\vec a,\;\vec b,\;\vec c\) không đồng phẳng là:
-
Câu 17:
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, AC, CD và DB.
Bộ ba vecto không đồng phẳng là:
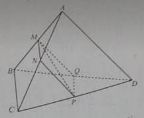
-
Câu 18:
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, AC, CD và DB.
Bộ ba vecto đồng phẳng là:
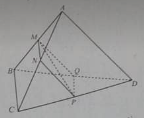
-
Câu 19:
Cho tứ diện ABCD có AB = AC = AD; góc BAC bằng góc BAD bằng 60o. Gọi M và N là trung điểm của AB và CD
Kết luận nào sau đây sai?
-
Câu 20:
Cho tứ diện ABCD có AB = AC = AD; góc BAC bằng góc BAD bằng 60o. Gọi M và N là trung điểm của AB và CD
Góc giữa \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) bằng:
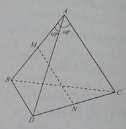
-
Câu 21:
Cho tứ diện ABCD. Nếu AB ⊥CD, AC ⊥ BD và BC ⊥ AD thì:
-
Câu 22:
Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh bằng a và các góc phẳng đỉnh B đều bằng 60o.
Đường thẳng B’C vuông góc với đường thẳng:
.png)
-
Câu 23:
Nếu ba vecto \(\vec a,\;\vec b,\overrightarrow c \) cùng vuông góc với vecto \(\vec n\) khác \(\vec 0\) thì chúng.
-
Câu 24:
Cho ba vecto \(\vec n,\;\vec a,\;\vec b\) bất kì đều khác với vecto \(\vec 0\). Nếu vecto \(\vec n\) vuông góc với cả hai vecto \(\vec a\) và \(\vec b\) thì \(\vec n\), \(\vec a\) và \(\vec b\):
-
Câu 25:
Cho vecto \(\vec n\; \ne \;\vec 0\) và hai vecto \(\vec a\) và \(\vec b\) không cùng phương. Nếu vecto \(\vec n\) vuông góc với cả hai vecto \(\vec a\) và \(\vec b\) thì \(\vec n\), \(\vec a\) và \(\vec b\):
-
Câu 26:
Cho tứ diện ABCD có AB = AC = AD; góc BAC = góc BAD = 60oBAD = 60o. Hãy chứng mình AB ⊥ CD.
Một bạn chứng mình qua các bước sau:
Bước 1. \(\overrightarrow {CD} \; = \;\overrightarrow {AC} \; - \;\overrightarrow {AD} \)
Bước 2. \(\overrightarrow {AB} .\overrightarrow {CD} \; = \;\overrightarrow {AB} .\left( {\overrightarrow {AC} \; - \;\overrightarrow {AD} } \right)\)
Bước 3. \(\overrightarrow {AB} .\overrightarrow {AC} \; - \;\overrightarrow {AB} .\overrightarrow {AD} \; = \;\left| {\overrightarrow {AB} \left| . \right|\overrightarrow {AD} \;} \right|.\cos {60^o}\; - \;\left| {\overrightarrow {AB} \left| . \right|\overrightarrow {AD} } \right|.\cos {60^o}\; = \;0\)
Bước 4. Suy ra AB ⊥ CD
Theo em. Lời giải trên sai từ:











