Cho hình lăng trụ tứ giác đều \(ABCD.A'B'C'D'\) có cạnh đáy bằng \(a\), góc giữa hai mặt phẳng \(\left( ABCD \right)\) và \(\left( ABC' \right)\) có số đo bằng \({{60}^{0}}\). Cạnh bên của hình lăng trụ bằng:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChọn C.
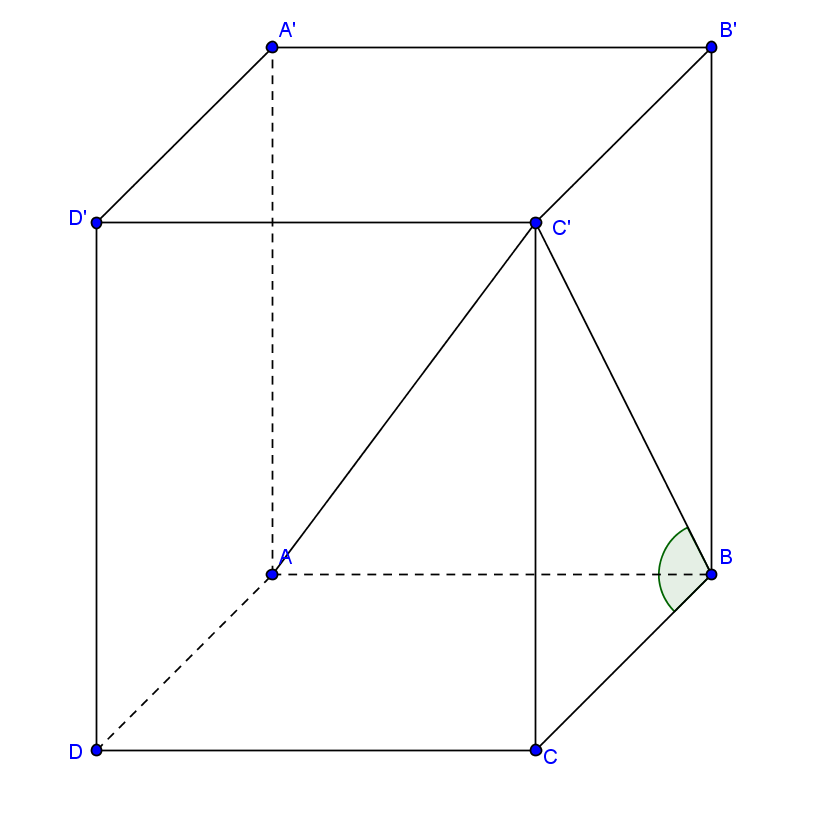
Ta có: \(CC'\bot \left( ABCD \right)\) và \(BC\bot AB\left( hv \right)\) \(\left( 1 \right)\)
Mặt khác:
\(\left\{ \begin{align} & AB\bot BC \\ & AB\bot BB' \\ \end{align} \right.\)
\(\Rightarrow \left\{ \begin{align} & AB\bot \left( BCC'B' \right) \\ & BC'\subset \left( BCC'B' \right) \\ \end{align} \right.\)
\(\Rightarrow AB\bot BC'\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra: \(\widehat{CBC'}={{60}^{0}}\) là góc giữa \(\left( ABC' \right)\) và \(\left( ABCD \right)\)
Xét \(\Delta BCC'\) vuông tại \(C\) có: \(\tan {{60}^{0}}=\frac{CC'}{BC}\Rightarrow CC'=BC.\tan {{60}^{0}}=a\sqrt{3}\).
Đề thi HK2 môn Toán 11 năm 2022-2023
Trường THPT Phan Bội Châu











