Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \cos 2x + \cos x.\) Khi đó \(M + m\) bằng bao nhiêu?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhương pháp giải:
- B1: Sử dụng công thức \(\cos 2x = 2{\cos ^2}x - 1\).
- B2: Đưa hàm số về dạng \(y = 2{\cos ^2}x + \cos x - 1\) sau đó đặt ẩn phụ và khảo sát hàm số.
Lời giải chi tiết:
TXĐ : \(D = \mathbb{R}\).
Ta có: \(y = \cos 2x + \cos x = 2{\cos ^2} + \cos x - 1\).
Đặt : \(t = \cos x\), \(t \in \left[ { - 1;1} \right]\).
Xét\(f\left( t \right) = 2{t^2} + t - 1\).
Đồ thị của hàm số \(f\) là parabol có đỉnh \(I\left( { - \frac{1}{4}; - \frac{9}{8}} \right)\).
BBT:
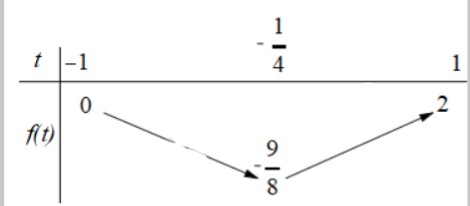
Dựa vào BBT ta có : \(M = \mathop {\max }\limits_{\left[ { - 1;1} \right]} f\left( t \right) = 2\), \(m = \mathop {\min }\limits_{\left[ { - 1;1} \right]} f\left( t \right) = - \frac{9}{8}\).
Vậy \(M + m = \frac{7}{8}\).
Đáp án A.
Đề thi giữa HK1 môn Toán 11 năm 2023 - 2024
Trường THPT Trần Hưng Đạo













