Đề thi giữa HK2 môn Toán 8 CTST năm 2023-2024
Trường THCS Trung Châu
-
Câu 1:
Chọn khẳng định sai?
A. \(y = 6x + 8\) có hệ số của \(x\) là 6 ; hệ số tự do là 8
B. \(y = - x - 5\) có hệ số của \(x\) là -1 ; hệ số tự do là -5
C. \(y = \frac{x}{3}\) có hệ số của \(x\) là \(\frac{1}{3}\); hệ số tự do là 1
D. \(y = 2 - 2x\) có hệ số của \(x\) là -2 , hệ số tự do là 2
-
Câu 2:
Tuổi bố hiện nay gấp 2,4 lần tuổi con. 5 năm trước đây, tuổi bố gấp \(\frac{{11}}{4}\) lần tuổi con. Tính tuổi con hiện nay?
A. 25 tuổi
B. 60 tuổi
C. 35 tuổi
D. 10 tuổi
-
Câu 3:
Với \(x = 7\) là nghiệm của phương trình nào dưới đây?
A. \(11 - 2x = x - 1\)
B. \(5x + 14 = - 2x\)
C. \(x - 9 = 5 - x\)
D. \(3x + 1 = 7x - 11\)
-
Câu 4:
Hai đường thẳng \(y = - 5x\) và \(y = - 5x + 2\)?
A. trùng nhau
B. song song
C. vuông góc
D. cắt nhau
-
Câu 5:
Cho tam giác \({\rm{ABC}}\) vuông tại \(A\) và có đường phân giác \(BD\left( {D \in AC} \right)\). Biết \(AD = 3{\rm{\;cm}},DC = 5{\rm{\;cm}}\). Tính độ dài các đoạn thẳng \({\rm{BC}}\)?
A. \(8{\rm{\;cm}}\)
B. \(13{\rm{\;cm}}\)
C. \(15{\rm{\;cm}}\)
D. \(10{\rm{\;cm}}\)
-
Câu 6:
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 5{\rm{\;cm}}\) và \(BC = 13{\rm{\;cm}}\). Qua trung điểm \(M\) của \({\rm{AB}}\), vẽ một đường thẳng song song với \({\rm{AC}}\) cắt \({\rm{BC}}\) tại \({\rm{N}}\). Tính độ dài \({\rm{MN}}\)?
A. \(6\left( {{\rm{\;m}}} \right)\)
B. \(7,5\left( {{\rm{\;m}}} \right)\)
C. \(2,5\left( {{\rm{\;m}}} \right)\)
D. \(10\left( {{\rm{\;m}}} \right)\)
-
Câu 7:
Trong hình dưới đây, độ dài đoạn thẳng \({\rm{A'C'}}\) mô tả chiều cao của một cái cây, đoạn thẳng \({\rm{AC}}\) mô tả chiều cao của một cái cọc (cây và cọc cùng vuông góc với đường thẳng đi qua ba điểm \(\left. {A',A,B} \right)\). Giả sử \(AC = 2{\rm{\;m}},AB = 1,5{\rm{\;m}},A'B = 4,5{\rm{\;m}}\). Tính chiều cao của cây?
A. \(1,5{\rm{\;m}}\)
B. \(6{\rm{\;m}}\)
C. \(7{\rm{\;m}}\)
D. \(5{\rm{\;m}}\)
-
Câu 8:
Một toà nhà cao \(24{\rm{\;m}}\), đổ bóng nắng dài \(36{\rm{\;m}}\) trên đường như hình sau. Một người cao 1,6 m muốn đứng trong bóng râm của toà nhà. Hỏi người đó có thể đứng cách toà nhà xa nhất bao nhiêu mét?
A. \(36,3{\rm{\;m}}\)
B. \(33,6{\rm{\;m}}\)
C. \(36{\rm{\;m}}\)
D. \(36,6{\rm{\;m}}\)
-
Câu 9:
Đường trung bình của tam giác?
A. Là đoạn thẳng nối hai điểm bất kì trên hai cạnh của tam giác
B. Là đoạn thẳng cắt hai cạnh của tam giác, song song với cạnh thứ ba và bằng nửa cạnh ấy
C. Là đường thẳng đi qua trực tâm của tam giác
D. Cả 3 ý trên đều sai
-
Câu 10:
Hàm số nào dưới đây không phải hàm số bậc nhất?
A. \(y = \sqrt 3 \left( {x + 1} \right)\)
B. \(y = 2 - 3x\)
C. \(y = 4{x^2}\)
D. \(y = - 5x\)
-
Câu 11:
Bác An đã gửi một lượng tiền tiết kiệm kì hạn 1 năm ở một ngân hàng với lãi suất 5,6%/năm (cứ sau kì hạn 1 năm, tiền lãi của kì hạn đó lại được cộng vào tiền vốn). Sau khi gửi 2 năm, bác An có được số tiền cả gốc và lãi là 111513600 đồng. Hỏi ban đầu bác An đã gửi vào ngân hàng số tiền là bao nhiêu đồng? Biết rằng lãi suất ngân hàng không thay đổi trong 2 năm đó.
A. 98 triệu đồng
B. 100 triệu đồng
C. 110 triệu đồng
D. 92 triệu đồng
-
Câu 12:
Cho tam giác \(MNP\) có \(MD\) là tia phân giác của góc \(M\left( {D \in NP} \right)\). Trong các khẳng định sau, khẳng định nào đúng?
A. \(\frac{{{\rm{DN}}}}{{{\rm{MN}}}} = \frac{{{\rm{DP}}}}{{{\rm{MP}}}}\)
B. \(\frac{{{\rm{DN}}}}{{{\rm{MN}}}} = \frac{{{\rm{MP}}}}{{{\rm{DP}}}}\)
C. \(\frac{{{\rm{MN}}}}{{{\rm{DN}}}} = \frac{{{\rm{DP}}}}{{{\rm{MP}}}}\)
D. \(\frac{{{\rm{MN}}}}{{{\rm{MP}}}} = \frac{{{\rm{DP}}}}{{{\rm{DN}}}}\)
-
Câu 13:
Cho các điểm \({\rm{A}}\left( { - 3;8} \right),{\rm{B}}\left( { - 2; - 5} \right),{\rm{C}}\left( {1;0} \right)\) và \({\rm{D}}\left( {\frac{1}{2};\frac{3}{4}} \right)\), điểm thuộc đồ thị của hàm số \(y = {x^2} - 1\) là?
A. \(B\left( { - 2; - 5} \right)\)
B. \(C\left( {0;1} \right)\)
C. \({\rm{D}}\left( {\frac{1}{2};\frac{3}{4}} \right)\)
D. \(A\left( { - 3;8} \right)\)
-
Câu 14:
Cho tam giác \({\rm{ABC}}\) Một đường thẳng \(d\) song song với \({\rm{BC}}\) và cắt các cạnh \({\rm{AB}},{\rm{AC}}\) của tam giác đó lần lượt tại \({\rm{M}},{\rm{N}}\) với \(\frac{{AM}}{{AB}} = \frac{1}{3}\) và \(AN + AC = 16{\rm{\;cm}}\). Tính \({\rm{AN}}\)?
A. \(4{\rm{\;cm}}\)
B. \(5{\rm{\;cm}}\)
C. \(6{\rm{\;cm}}\)
D. \(7{\rm{\;cm}}\)
-
Câu 15:
Để làm cây thông noel, người ta hàn một khung sắt có dạng hình tam giác cân \({\rm{ABC}}\left( {AB = AC = 2{\rm{\;m}}} \right)\) cùng các thanh sắt nằm ngang \({\rm{GF}},{\rm{HE}},{\rm{ID}},{\rm{BC}}\) và sau đó gắn cây thông như như hình vẽ. Tính số tiền sắt cần sử dụng để làm cây thông noel đó. Biết giá một mét sắt là 55000 đồng và \(AG = GH = HI = IB,CD = DE = EF = FA\), thanh \(GF\) dài \(0,2{\rm{\;m}}\).

A. 303000 đồng
B. 300000 đồng
C. 333000 đồng
D. 330000 đồng
-
Câu 16:
Toà nhà Bitexco Financial (hay tháp tài chính Bitexco) được xây dựng tại trung tâm Quận 1, Thành phố Hồ Chí Minh. Toà nhà có 68 tầng (không kể các tầng hầm). Biết rằng khi toà nhà có bóng MP in trên mặt đất dài \(47,5{\rm{\;m}}\), thì cùng thời điểm đó một cột cờ \({\rm{AB}}\) cao \(12{\rm{\;m}}\) có bóng \({\rm{AP}}\) in trên mặt đất dài \(2,12{\rm{\;m}}\). Tính chiều cao \({\rm{MN}}\) của toà nhà theo đơn vị mét (làm tròn kết quả đến hàng đơn vị).
A. \(268\left( {{\rm{\;m}}} \right)\)
B. \(269\left( {{\rm{\;m}}} \right)\)
C. \(266\left( {{\rm{\;m}}} \right)\)
D. 267 (m)
-
Câu 17:
Cho tam giác \({\rm{ABC}}\) có \(AB = 4,5{\rm{\;cm}},AC = 6{\rm{\;cm}}\). Các điểm \({\rm{M}},{\rm{N}}\) lần lượt thuộc các cạnh \({\rm{AB}},{\rm{AC}}\) thoả mãn \(AM = 3{\rm{\;cm}}\) và \(MN\parallel BC\). Tính độ dài đoạn thẳng \({\rm{AN}}\)?
A. \(3,5{\rm{\;cm}}\)
B. \(5{\rm{\;cm}}\)
C. \(4{\rm{\;cm}}\)
D. \(6,5{\rm{\;cm}}\)
-
Câu 18:
Chọn phát biểu đúng?
A. Hàm số bậc nhất có dạng \(y = ax + b\), trong đó \({\rm{a}},{\rm{b}}\) là các số cho trước
B. Hàm số bậc nhất có dạng \(y = ax + b\), trong đó \({\rm{a}},{\rm{b}}\) là các số cho trước và \(a,b \ne 0\)
C. Hàm số bậc nhất có dạng \(y = ax + b\), trong đó \({\rm{a}},{\rm{b}}\) là các số cho trước và \(b \ne 0\)
D. Hàm số bậc nhất có dạng \(y = ax + b\), trong đó \({\rm{a}},{\rm{b}}\) là các số cho trước và \(a \ne 0\)
-
Câu 19:
Đáp án nào dưới đây không là phương trình bậc nhất một ẩn?
A. \(3x + \frac{3}{5} = 0\)
B. \(\frac{2}{3}y - 7 = 0\)
C. \(7 = 2t\)
D. \({z^2} - 9 = 0\)
-
Câu 20:
Cho các đường thẳng \({d_1}:y = 11x + 1;{d_2}:y = \sqrt 3 x - 7;{d_3}:y = 2x - \sqrt 2 \). Gọi \({\alpha _1},{\alpha _2},{\alpha _3}\) lần lượt là các góc tạo bởi đường thẳng \({d_1},{d_2},{d_3}\) và trục \({\rm{Ox}}\). Sắp xếp các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) theo thứ tự số đo tăng dần?
A. \({\alpha _2} < {\alpha _3} < {\alpha _1}\)
B. \({\alpha _1} < {\alpha _3} < {\alpha _2}\)
C. \({\alpha _1} < {\alpha _2} < {\alpha _3}\)
D. \({\alpha _2} < {\alpha _1} < {\alpha _3}\)
-
Câu 21:
Cho hai đường thẳng \(d:y = mx - \left( {2m + 2} \right)\) và \(d':y = \left( {3 - 2m} \right)x + 1\) với \(m \ne 0\) và \(m \ne \frac{3}{2}\) Tìm giá trị của \(m\) để \(d\) và \(d\) ' cắt nhau?
A. \(m \ne 1\)
B. \(m \ne 0,m \ne \frac{3}{2}\)
C. \(m \ne 0,m \ne \frac{3}{2},m \ne 1\)
D. \(m \ne 0,m \ne \frac{3}{2},m \ne - 1\)
-
Câu 22:
Cho hình sau với tam giác \({\rm{ABC}}\) có \(AB = AC = 9{\rm{\;cm}}\) và tia phân giác của góc \(B\) cắt đường cao \({\rm{AH}}\) ở \(I\) Biết \(\frac{{AI}}{{IH}} = \frac{3}{2}\). Tính chu vi tam giác \({\rm{ABC}}\)?
A. \(35{\rm{\;cm}}\)
B. \(29{\rm{\;cm}}\)
C. \(30{\rm{\;cm}}\)
D. \(32{\rm{\;cm}}\)
-
Câu 23:
Câu ca dao "Lúa chiêm lấp ló đầu bờ - Hễ nghe tiếng sấm phất cờ mà lên" về mặt khoa học được giải thích như sau: Khi trời mưa kèm theo sấm sét, nitric acid sẽ được sinh ra và hoà tan trong nước mưa, có tác dụng làm tăng cường dinh dưỡng nitrogen cho đất trồng, giúp cây lúa phát triển tươi tốt. Phân tử của nitric acid đó có một nguyên tử \({\rm{H}}\), một nguyên tử \({\rm{N}}\) và \(x\) nguyên tử \({\rm{O}}\). Xác định công thức phân tử của nitric acid đó. Biết khối lượng phân tử của nó là 63amu và khối lượng của mỗi nguyên tử \({\rm{H}},{\rm{N}},{\rm{O}}\) lần lượt là 1amu, 14amu, 16amu .
A. \(HNO\)
B. \({\rm{HN}}{{\rm{O}}_4}\)
C. \({\rm{HN}}{{\rm{O}}_2}\)
D. \({\rm{HN}}{{\rm{O}}_3}\)
-
Câu 24:
Một ao sen có dạng hình thang \(ABCD\left( {AB//CD} \right)\) với \(AB = 35{\rm{\;m}},CD = 56{\rm{\;m}}\). Người ta chọn một vị trí \(E\) ở trên bờ \({\rm{AD}}\) sao cho \(AE = \frac{3}{4}ED\) và bắc một cây cầu \({\rm{EF}}\) song song với hai bờ \(AB,CD\left( {F \in BC} \right)\). Để mọi người có thể đi trên cầu buổi tối ngắm sen, người ta căng đèn trang trí dọc theo cây cầu đó với khoảng cách giữa hai chiếc đèn liên tiếp là \(2{\rm{\;m}}\) và cả hai đầu cầu đều có đèn. Tính số tiền cần dùng để mua đèn trang trí cho cây cầu đó, biết giá mỗi chiếc đèn là 15000 đồng.
A. 345000 đồng
B. 330000 đồng
C. 300000 đồng
D. 310000 đồng
-
Câu 25:
Cho đường thẳng d: y = 2x + 1. Hệ số góc của đường thẳng d là?
A. -2
B. 1
C. \(\frac{1}{2}\)
D. 2
-
Câu 26:
Cho đường thẳng d : y = -3x + 2. Gọi A, B lần lượt là giao điểm của d với trục hoành và trục tung. Diện tích tam giác OAB là?
A. \(\frac{4}{3}\)
B. \(\frac{{ - 2}}{3}\)
C. \(\frac{3}{2}\)
D. \(\frac{2}{3}\)
-
Câu 27:
Cho hàm số \(y = f\left( x \right) = \frac{1}{2}x + 5\), giá trị \(f\left( 0 \right)\) là?
A. -5
B. 0
C. 5
D. 10
-
Câu 28:
Cho \(y = \left( {m - 3} \right)x + 7\), hàm số không phải là hàm bậc nhất khi m bằng?
A. 1
B. 3
C. -3
D. 0
-
Câu 29:
Cho\(y = \left( {m + 3} \right)x - 2\), giá trị của m để hàm số có hệ số góc âm trên \(\mathbb{R}\) là?
A. 0
B. 3
C. -1
D. -4
-
Câu 30:
Góc tạo bởi đường thẳng \(y = - x + 5\) và trục Ox là?
A. \({45^0}\)
B. \({90^0}\)
C. \({120^0}\)
D. \({60^0}\)
-
Câu 31:
Tam giác ABC có M, N lần lượt là trung điểm của AB, AC. Vẽ ME, NF cùng vuông góc với BC (E, F thuộc BC). Khẳng định sai là?
A. MN // EF
B. ME = NF
C. MN = ME
D. MN = EF
-
Câu 32:
Cho tam giác ABC có chu vi 80cm. Gọi D, E, F là trung điểm của các cạnh AB, AC, BC. Chu vi tam giác DEF là?
A. 40cm
B. 160cm
C. 80cm
D. 20cm
-
Câu 33:
Giá trị của x là?
A. 6
B. 4
C. 2
D. 1
-
Câu 34:
Để tính chiều cao AB của ngôi nhà (như hình vẽ), người ta đo chiều cao của cái cây ED = 2m và biết được các khoảng cách AE = 4m, EC = 2,5m.
Khi đó chiều cao AB của ngôi nhà là?
A. 5,2m
B. 8,125m
C. 4m
D. 6,5m
-
Câu 35:
Cho hình vẽ:
Giá trị của x là?
A. 10
B. 5,5
C. 3
D. 1,75
-
Câu 36:
Cho hình vẽ:
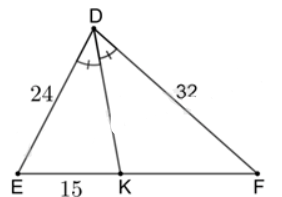
Độ dài KF là?
A. 20
B. 51,2
C. 15
D. 11,25
-
Câu 37:
Nhà bác học Galileo Galilei (1564 – 1642) là người đầu tiên phát hiện ra quan hệ giữa quãng đường chuyển động y (m) và thời gian chuyển động x (giây) của một vật được biểu diễn gần đúng bởi hàm số \(y = 5{x^2}\). Quãng đường mà vật đó chuyển động được sau 3 giây là?
A. 20m
B. 45m
C. 50m
D. 60m
-
Câu 38:
Cho hình vẽ bên. Đường thẳng OK là đồ thị của hàm số?
A. \(y = - 2 x \)
B. \(y = - 0,5x\)
C. \(y = \frac{1}{2}x\)
D. \(y = 2 x\)
-
Câu 39:
Xác định đường thẳng \(y = ax + b;(a \ne 0)\) có hệ số góc bằng 2 và đi qua điểm A (2;1)?
A. \(y = - 2x + 3\)
B. \(y = 2x - 3\)
C. \(y = - 2x - 3\)
D. \(y = 2x + 5\)
-
Câu 40:
“Trên mặt phẳng, ta vẽ hai trục số Ox, Oy …… với nhau và ……. tại gốc tọa độ O của mỗi trục. Khi đó ta có hệ trục tọa độ Oxy”. Các từ lần lượt cần điền đó là?
A. song song; vuông góc
B. vuông góc; trùng nhau
C. vuông góc; cắt nhau
D. trùng; cắt nhau
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)
.PNG)











