Đề thi HK1 môn Toán 10 năm 2020
Trường THPT Hoàng Hoa Thám
-
Câu 1:
Cho tập hợp \(A = \left[ { - \sqrt 3 ;\,\sqrt 5 } \right)\). Tìm tập hợp \({C_R}A\).
A. \(\left( { - \infty ;\, - \sqrt 3 } \right] \cup \left( {\sqrt 5 ;\, + \infty } \right)\)
B. \(\left( { - \infty ;\, - \sqrt 3 } \right) \cup \left( {\sqrt 5 ;\, + \infty } \right)\)
C. \(\left( { - \infty ;\, - \sqrt 3 } \right] \cup \left[ {\sqrt 5 ;\, + \infty } \right)\)
D. \(\left( { - \infty ;\, - \sqrt 3 } \right) \cup \left[ {\sqrt 5 ;\, + \infty } \right)\)
-
Câu 2:
Phát biểu nào sau đây là một mệnh đề?
A. Mùa thu Hà Nội đẹp quá!
B. Bạn có đi học không?
C. Đề thi môn Toán khó quá!
D. Hà Nội là thủ đô của Việt Nam.
-
Câu 3:
Cho \(A = \left\{ {x \in {N^*},x < 10,\,\,x \vdots 3} \right\}\). Chọn khẳng định đúng.
A. A có 4 phần tử
B. A có 3 phần tử
C. A có 5 phần tử
D. A có 2 phần tử
-
Câu 4:
Tập \(\left( { - \infty ; - 3} \right) \cap \left[ { - 5;2} \right)\) bằng tập nào dưới đây?
A. \(\left[ { - 5; - 3} \right)\)
B. \(\left( { - \infty ; - 5} \right]\)
C. \(\left( { - \infty ; - 2} \right)\)
D. \(\left( { - 3; - 2} \right)\)
-
Câu 5:
Hình vẽ sau đây (phần không bị gạch) là biểu diễn của tập hợp nào?
A. \(\left( { - \infty ; - 2} \right) \cup \left[ {5; + \infty } \right)\)
B. \(\left( { - \infty ; - 2} \right) \cup \left( {5; + \infty } \right)\)
C. \(\left( { - \infty ; - 2} \right] \cup \left( {5; + \infty } \right)\)
D. \(\left( { - \infty ; - 2} \right] \cup \left[ {5; + \infty } \right)\)
-
Câu 6:
Khi sử dụng máy tính bỏ túi với 10 chữ số thập phân ta được: \(\sqrt 8 = 2,828427125\). Giá trị gần đúng của \(\sqrt 8 \) chính xác đến hàng phần trăm là giá trị nào dưới đây?
A. 2,81
B. 2,80
C. 2,82
D. 2,83
-
Câu 7:
Cho các phát biểu sau đây:
(I): “17 là số nguyên tố”
(II): “Tam giác vuông có một đường trung tuyến bằng nửa cạnh huyền”
(III): “Các em C14 hãy cố gắng học tập thật tốt nhé !”
(IV): “Mọi hình chữ nhật đều nội tiếp được đường tròn”
Hỏi có bao nhiêu phát biểu là mệnh đề?
A. 4
B. 3
C. 2
D. 1
-
Câu 8:
Cho mệnh đề “Có một học sinh trong lớp C4 không chấp hành luật giao thông”. Mệnh đề phủ định của mệnh đề này là mệnh đề nào sau đây?
A. Không có học sinh nào trong lớp C4 chấp hành luật giao thông.
B. Mọi học sinh trong lớp C4 đều chấp hành luật giao thông.
C. Có một học sinh trong lớp C4 chấp hành luật giao thông.
D. Mọi học sinh trong lớp C4 không chấp hành luật giao thông.
-
Câu 9:
Đo chiều dài của một cây thước, ta được kết quả \(\overline a = 45 \pm 0,3\,({\rm{cm}})\). Khi đó sai số tuyệt đối của phép đo được ước lượng là bao nhiêu?
A. \({\Delta _{45}} = 0,3\)
B. \({\Delta _{45}} \le 0,3\)
C. \({\Delta _{45}} \le - 0,3\)
D. \({\Delta _{45}} = - 0,3\)
-
Câu 10:
Cho hai tập hợp \(X = \left\{ {1\,;\,2\,;\,4\,;\,7\,;\,9} \right\}\) và \(X = \left\{ { - 1\,;\,0\,;\,7\,;\,10} \right\}\). Tập hợp \(X \cup Y\) có bao nhiêu phần tử?
A. 9
B. 7
C. 8
D. 10
-
Câu 11:
Cho các tập hợp A, B, C được minh họa bằng biểu đồ Ven như hình bên. Phần tô màu xám trong hình là biểu diễn của tập hợp nào sau đây?
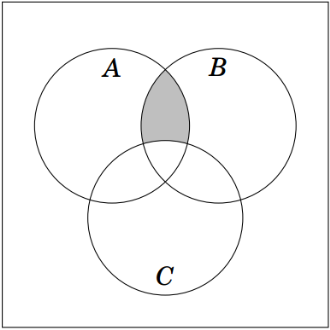
A. \(A \cap B \cap C\)
B. \(\left( {A\backslash C} \right) \cup \left( {A\backslash B} \right)\)
C. \(\left( {A \cup B} \right)\backslash C\)
D. \(\left( {A \cap B} \right)\backslash C\)
-
Câu 12:
Tìm tập xác định của hàm số \(y = \sqrt {x - 2} + \dfrac{{2x + 5}}{{x - 4}}\).
A. D = R \ {4}
B. D = R \ {2}
C. \(D = \left( { - \infty ;2} \right]\)
D. \(D = \left[ {2; + \infty } \right)\backslash \left\{ 4 \right\}\)
-
Câu 13:
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l} - 2\left( {x - 2} \right)\,\,khi\, - 1 \le x < 1\\ \sqrt {{x^2} - 1} \,\,\,\,\,\,khi\,\,x \ge 1 \end{array} \right.\). Giá trị \(f\left( { - 1} \right)\) bằng bao nhiêu?
A. -6
B. 6
C. 5
D. -5
-
Câu 14:
Xét tính chẵn, lẻ của hai hàm số \(f\left( x \right) = \left| {x + 2} \right|--\left| {x - 2} \right|,g\left( x \right) = --\left| x \right|\).
A. f(x) là hàm số chẵn, g(x) là hàm số chẵn.
B. f(x) là hàm số lẻ, g(x) là hàm số chẵn.
C. f(x) là hàm số lẻ, g(x) là hàm số lẻ.
D. f(x) là hàm số chẵn, g(x) là hàm số lẻ.
-
Câu 15:
Xét sự biến thiên của hàm số \(y = \dfrac{1}{{{x^2}}}\). Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên \(\left( { - \infty ;0} \right)\), nghịch biến trên \(\left( {0; + \infty } \right)\).
B. Hàm số đồng biến trên \(\left( {0; + \infty } \right)\), nghịch biến trên \(\left( { - \infty ;0} \right)\).
C. Hàm số đồng biến trên \(\left( { - \infty ;1} \right)\), nghịch biến trên \(\left( {1; + \infty } \right)\).
D. Hàm số nghịch biến trên \(\left( { - \infty ;0} \right) \cup \left( {0; + \infty } \right)\).
-
Câu 16:
Hình vẽ sau đây là đồ thị của hàm số nào?
A. y = |x|
B. y = |x| + 1
C. y = 1 - |x|
D. y = |x| - 1
-
Câu 17:
Cho hàm số y = x - |x|. Trên đồ thị của hàm số lấy hai điểm A và B có hoành độ lần lượt là -2 và 1. Phương trình đường thẳng là phương trình nào dưới đây?
A. \(y = \frac{{3x}}{4} - \frac{3}{4}\)
B. \(y = \frac{{4x}}{3} - \frac{4}{3}\)
C. \(y = - \frac{{3x}}{4} + \frac{3}{4}\)
D. \(y = - \frac{{3x}}{2} + \frac{1}{2}\)
-
Câu 18:
Tìm tọa độ giao điểm của hai đường thẳng \(y = x + 2\) và \(y = - \frac{3}{4}x + 3\).
A. \(\left( {\frac{4}{7};\frac{{18}}{7}} \right)\)
B. \(\left( {\frac{4}{7}; - \frac{{18}}{7}} \right)\)
C. \(\left( { - \frac{4}{7};\frac{{18}}{7}} \right)\)
D. \(\left( { - \frac{4}{7}; - \frac{{18}}{7}} \right)\)
-
Câu 19:
Trong mặt phẳng tọa độ Oxy cho đường thẳng có phương trình \(y = kx + {k^2}-3\). Tìm k để đường thẳng (d) đi qua gốc tọa độ.
A. \(k = \sqrt 3 \)
B. \(k = \sqrt 2\)
C. \(k = -\sqrt 2\)
D. \(k = \sqrt 3\) hoặc \(k =- \sqrt 3\)
-
Câu 20:
Hàm số \(y = \left| {x + 1} \right| + \left| {x - 3} \right|\) được viết lại là:
A. \(y = \left\{ \begin{array}{l} - 2x + 2\,\,\,\,khi\,\,\,\,x \le - 1\\ 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,\,\, - 1 < x \le 3\\ 2x - 1\,\,\,\,\,\,\,khi\,\,\,\,x > 3 \end{array} \right.\)
B. \(y = \left\{ \begin{array}{l} 2x - 2\,\,\,\,\,\,\,khi\,\,\,\,x \le - 1\\ 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,\, - 1 < x \le 3\\ - 2x + 2\,\,\,khi\,\,\,x > 3 \end{array} \right.\)
C. \(y = \left\{ \begin{array}{l} 2x + 2\,\,\,\,\,\,\,\,khi\,\,\,\,x \le - 1\\ 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,\, - 1 < x \le 3\\ - 2x - 2\,\,\,\,khi\,\,\,\,\,x > 3 \end{array} \right.\)
D. \(y = \left\{ \begin{array}{l} - 2x + 2\,\,\,\,khi\,\,\,x \le - 1\\ 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,\,\, - 1 < x \le 3\\ 2x - 2\,\,\,\,\,\,khi\,\,\,\,x > 3 \end{array} \right.\)
-
Câu 21:
Tìm tất cả các giá trị thực của m để phương trình \(- 2{x^2} - 4x + 3 = m\) có nghiệm.
A. \(1 \le m \le 5\)
B. \(- 4 \le m \le 0\)
C. \(0 \le m \le 4\)
D. \(m \le 5\)
-
Câu 22:
Cho parabol \(\left( P \right):y = {x^2} + x + 2\) và đường thẳng \(d:y = ax + 1.\) Tìm tất cả các giá trị thực của a để (P) tiếp xúc với d.
A. a = -1; a = 3
B. a = 2
C. a = 1; a = -3
D. Không tồn tại a
-
Câu 23:
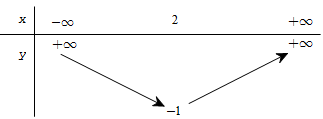
Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\) có bảng biến thiên như sau:
Tìm tất cả các giá trị thực của tham số m để phương trình \(f\left( x \right) - 1 = m\) có đúng hai nghiệm.
A. m > -1
B. m > 0
C. m > -2
D. \(m \ge - 1\)
-
Câu 24:
Cho hàm số \(f\left( x \right) = {x^2} - 6x + 1\). Khi đó kết luận nào sau đây là đúng?
A. f(x) tăng trên khoảng \(\left( { - \infty ;3} \right)\) và giảm trên khoảng \(\left( {3; + \infty } \right)\)
B. f(x) giảm trên khoảng \(\left( { - \infty ;3} \right)\) và tăng trên khoảng \(\left( {3; + \infty } \right)\)
C. f(x) luôn tăng
D. f(x) luôn giảm
-
Câu 25:
Cho parabol \(\left( P \right):y = - 3{x^2} + 6x - 1\). Tìm khẳng định đúng nhất trong các khẳng định sau.
A. (P) có đỉnh I(1;2)
B. (P) có trục đối xứng x = 1
C. (P) cắt trục tung tại điểm A(0; -1)
D. Cả A, B, C đều đúng.
-
Câu 26:
Tập xác định của phương trình \(\frac{{2x}}{{3 - x}} + \frac{1}{{2x - 1}} = \frac{{6 - 5x}}{{3x - 2}}\) là tập nào dưới đây?
A. \(\left( {3; + \infty } \right)\)
B. \(\left[ {3; + \infty } \right)\)
C. \(R\backslash \left\{ {\frac{1}{2};3;\frac{2}{3}} \right\}\)
D. \(R\backslash \left\{ {\frac{1}{2};3;\frac{3}{2}} \right\}\)
-
Câu 27:
Tìm m để phương trình \(\left( {{m^2}--2} \right)\left( {x + 1} \right) = x + 2\) vô nghiệm.
A. m = 0
B. \(m=\pm1\)
C. \(m=\pm2\)
D. \(m{\rm{ }} = \pm \sqrt[{}]{3}\)
-
Câu 28:
Hiện tại tuổi cha của An gấp 3 lần tuổi của An, 5 năm trước tuổi cha An gấp 4 lần tuổi An. Hỏi cha An sinh An lúc bao nhiêu tuổi?
A. 30
B. 25
C. 35
D. 28
-
Câu 29:
Có bao nhiêu giá trị của tham số m để phương trình \(\frac{{{x^2} + mx + 2}}{{{x^2} - 1}} = 1\) vô nghiệm?
A. 0
B. 1
C. 2
D. 3
-
Câu 30:
Tìm giá trị thực của tham số m để phương trình \(\left| x \right| + 1 = {x^2} + m\) có nghiệm duy nhất.
A. m = 0
B. m = 1
C. m = -1
D. Không có m
-
Câu 31:
Cho \(\overrightarrow {AB} \ne \vec 0\) và một điểm C. Có bao nhiêu điểm D thỏa mãn \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right|?\)
A. Vô số
B. 0
C. 1
D. 2
-
Câu 32:
Cho tam giác ABC và một điểm M tùy ý. Chứng minh rằng vectơ \(\overrightarrow v = \overrightarrow {MA} + \overrightarrow {MB} - 2\overrightarrow {MC} \). Hãy xác định vị trí của điểm D sao cho \(\overrightarrow {CD} = \overrightarrow v \).
A. D là điểm thứ tư của hình bình hành ABCD.
B. D là điểm thứ tư của hình bình hành ACBD.
C. D là trọng tâm của tam giác ABC
D. D là trực tâm của tam giác ABC
-
Câu 33:
Cho ba vectơ \(\vec a = \left( {2;{\rm{ }}1} \right),\vec b\left( {3;{\rm{ }}4} \right),\vec c = \left( {7;{\rm{ }}2} \right)\). Giá trị của k, h để \(\vec c = k.\vec a + h.\vec b\) là giá trị nào sau đây?
A. \(k = 2,5;{\rm{ }}h = - 1,3.\)
B. \(k = 4,6;{\rm{ }}h = - 5,1.\)
C. \(k = 4,4;{\rm{ }}h = - 0,6.\)
D. \(k = 3,4;{\rm{ }}h = - 0,2.\)
-
Câu 34:
Trong hệ tọa độ Oxy cho bốn điểm A(1;1), B(2;-1), C(4;3), D(3;5). Khẳng định nào sau đây đúng?
A. Tứ giác ABCD là hình bình hành.
B. \(G\left( {2;{\rm{ }}\frac{5}{3}} \right)\) là trọng tâm tam giác BCD.
C. \(\overrightarrow {AB} = \overrightarrow {CD} .\)
D. \(\overrightarrow {AC} ,{\rm{ }}\overrightarrow {AD} \) cùng phương
-
Câu 35:
Trong hệ tọa độ Oxy cho ba điểm A(2;1), B(0;-3), C(3;1). Tìm tọa độ điểm D để ABCD là hình bình hành.
A. (5;5)
B. (5;-2)
C. (5;-4)
D. (-1;-4)
-
Câu 36:
Trong hệ tọa độ Oxy cho tam giác ABC có \(M\left( {2;{\rm{ }}3} \right),{\rm{ }}N\left( {0;{\rm{ }} - 4} \right),{\rm{ }}P\left( { - 1;{\rm{ }}6} \right)\) lần lượt là trung điểm của các cạnh \(BC,CA,AB\). Tìm tọa độ đỉnh A?
A. (1;5)
B. (-3;-1)
C. (-2;-7)
D. (1;-10)
-
Câu 37:
Cho hai điểm A(-3;2), B(4;3). Tìm điểm M thuộc trục Ox và có hoành độ dương để tam giác MAB vuông tại M.
A. M(7;0)
B. M(5;0)
C. M(3;0)
D. M(9;0)
-
Câu 38:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(5;5), B(-3;1), C(1;-3). Diện tích tam giác ABC.
A. S = 24
B. S = 2
C. \(S = 2\sqrt 2 \)
D. S = 12
-
Câu 39:
Cho \(\overrightarrow a \) và \(\overrightarrow b\) là hai véctơ cùng hướng và đều khác véctơ \(\overrightarrow 0\). Trong các kết quả sau đây, hãy chọn kết quả đúng.
A. \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\)
B. \(\overrightarrow a .\overrightarrow b = 0\)
C. \(\overrightarrow a .\overrightarrow b = - 1\)
D. \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\)
-
Câu 40:
Tam giác ABC có A(-1;1), B(1;3) và C(1;-1). Trong các phát biểu sau đây, hãy chọn phát biểu đúng.
A. ABC là tam giác đều.
B. ABC là tam giác có ba góc đều nhọn.
C. ABC là tam giác cân tại B (BA = BC)
D. ABC là tam giác vuông cân tại A
.PNG)
.PNG)