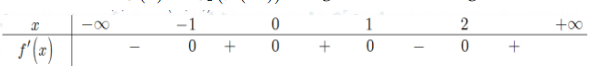Cho hàm số f(x) có bảng xét dấu đạo hàm như sau
Xét hàm số \(g(x)=f(1-x)+3^{\frac{1}{3} x^{3}-\frac{3}{2} x^{2}+2 x}\) . Khẳng định nào sau đây đúng?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(g^{\prime}(x)=-f^{\prime}(1-x)+3^{\frac{1}{3} x^{3}-\frac{3}{2} x^{2}+2 x}\left(x^{2}-3 x+2\right) \ln 3\)
Hàm số g(x) đồng biến khi \(g^{\prime}(x) \geq 0 \Leftrightarrow-f^{\prime}(1-x)+3^{\frac{1}{3} x^{3}-\frac{3}{2} x^{2}+2 x}\left(x^{2}-3 x+2\right) \ln 3 \geq 0\)
Ta có:
\(-f^{\prime}(1-x) \geq 0 \Leftrightarrow f^{\prime}(1-x) \leq 0 \Leftrightarrow\left[\begin{array}{l} 0 \leq 1-x \leq 1 \\ 1-x \leq-2 \end{array} \Leftrightarrow\left[\begin{array}{l} 0 \leq x \leq 1 \\ x \geq 3 \end{array}\right.\right.\)
Và \(3^{\frac{1}{3} x^{3}-\frac{3}{2} x^{2}+2 x}\left(x^{2}-3 x+2\right) \ln 3 \geq 0 \Leftrightarrow\left[\begin{array}{l} x \leq 1 \\ x \geq 2 \end{array}\right.\)
Suy ra trên \((3 ;+\infty) \text { thì } g^{\prime}(x)>0\)
Do đó hàm số g(x) đồng biến trên khoảng \((3 ;+\infty)\)