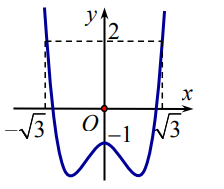
Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau

Biết rằng \(1<f(x)<5, \forall x \in R\) Hàm số \(g(x)=f(f(x)-1)+x^{3}+3 x^{2}+2020\) nghịch biến trên khoảng nào dưới đây

Câu hỏi liên quan

• . Hàm số \(y=f(x)=-x^3+3x^2-1\) đồng biến trên các khoảng:

• Hàm số \(y=\frac{x+2}{x-1}\)nghịch biến trên các khoảng:

   

• Tìm tất cả các giá trị thực của m để hàm số \(y = {2^{{x^3} – {x^2} + mx + 1}}\) đồng biến trên \(\left( {1;2} \right)\).

ZUNIA12

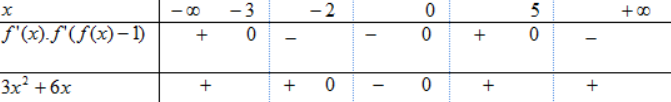•  Cho hàm số \(y=\frac{mx+2m–3}{x–m}\) (m là tham số). Tìm tất cả các giá trị của m sao cho hàm số nghịch biến trên khoảng \((2;+\infty)\)

• Cho phương trình x³- 3x²+ 1- m = 0  (1) . Điều kiện của tham số m để (1) có ba nghiệm phân biệt thỏa mãn x₁ < 1< x₂ < x₃ khi

• Hỏi hàm số nào sau đây luôn nghịch biến trên \(\mathbb{R}\) ?

• Tìm tập hợp tất cả các giá trị của m để hàm số \(y=\frac{2 x+1}{x+m}\) nghịch biến trên khoảng \((3 ;+\infty) \text { . }\)

• Có bao nhiêu giá trị nguyên của tham số m sao cho hàm số \(f(x) = \frac{1}{3}{x^3} + m{x^2} + 4x + 3\) đồng biến trên \(\mathbb{R}\).

• Hỏi hàm số nào sau đây luôn nghịch biến trên R?

• Tập hợp tất cả các giá trị thực của tham số m để hàm số \(y = {x^3} – 3{x^2} + \left( {2 – m} \right)x\) đồng biến trên khoảng \(\left( {2; + \infty } \right)\) là

• Có bao nhiêu số nguyên \(m \in(-2020 ; 2020)\) để hàm số \(y=\frac{\cos x+1}{10 \cos x+m}\) đồng biến trên khoảng \(\left(0 ; \frac{\pi}{2}\right) ?\)

• Cho hàm số y=f(x). Đồ thị hàm y=f'(x) như hình vẽ

  

  Đặt \(g(x)=3 f(x)-x^{3}+3 x-m\) với m là tham số thực. Điều kiện cần và đủ để bất phương trình \(g(x) \geq 0\) đúng với \(\forall x \in[-\sqrt{3} ; \sqrt{3}]\) là

• Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số \(y = \ln \left( {{x^2} + 1} \right) - mx + 1\) đồng biến trên khoảng ( -∞; +∞).

• Gọi S là tập hợp các giá trị nào của tham số m để hàm số \(y=\frac{(m+1) x+2 m+2}{x+m}\) nghịch biến trên khoảng \((-1 ;+\infty)\). Khi đó S là tập con của tập nào sau đây? 

• Hàm số y = x³ – 3x đồng biến trên khoảng nào?

• Hàm số \(y = - \frac{2}{3}{x^3} + 3{x^2} - x + 1\) đồng biến trên các khoảng: 

• Hàm số \(y=f(x)=\frac{x}{x-2}\) nghịch biến trên khoảng nào sau?

• Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2} – 2x, \forall x \in \mathbb{R}\). Hàm số \(y = – 2f\left( x \right)\) đồng biến trên khoảng

• Cho hàm số \(y = \frac{{ - x + 5}}{{x + 2}}\). Mệnh đề nào sau đây là đúng?

• Cho hàm số \(y=\frac{m x+9}{x+m}\) ( m là tham số thực). Tìm các giá trị của m để hàm số đã cho nghịch biến trên khoảng \((-\infty ; 1) ?\)