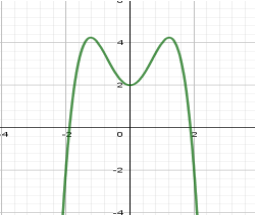
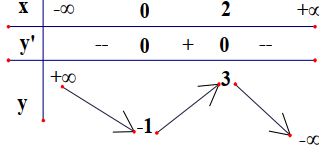
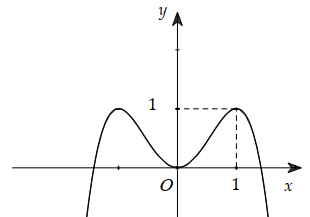
Cho hàm số y=f(x) có đạo hàm trên \(\mathbb{R}\) và có đồ thị là đường cong như hình vẽ. Đặt \(g(x)=3 f(f(x))+4\)
Tìm số điểm cực trị của hàm số g (x)?
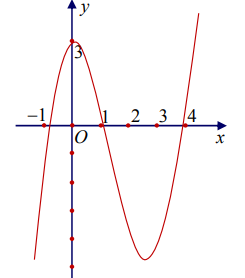
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai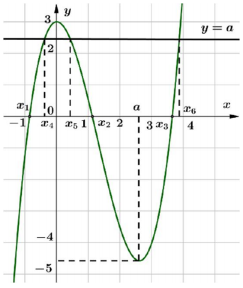
\(g^{\prime}(x)=3 f^{\prime}(f(x)) \cdot f^{\prime}(x)\).
\(g^{\prime}(x)=0 \Leftrightarrow 3 f^{\prime}(f(x)) \cdot f^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l} f^{\prime}(f(x))=0 \\ f^{\prime}(x)=0 \end{array} \Leftrightarrow\left[\begin{array}{l} f(x)=0 \\ f(x)=a \\ x=0 \\ x=a \end{array},(2<a<3)\right.\right.\)
f '(x)=0 có 3 nghiệm đơn phân biệt \(x_{1}, x_{2}, x_{3}\) khác 0 và a .
Vì 2<a<3 nên f (x)=a có 3 nghiệm đơn phân biệt \(x_{4}, x_{5}, x_{6}\) khác \(x_{1}, x_{2}, x_{3}, 0, a\)
Suy ra \(g^{\prime}(x)=0\) có 8 nghiệm đơn phân biệt. Do đó hàm số \(g(x)=3 f(f(x))+4\) có 8 điểm cực trị.