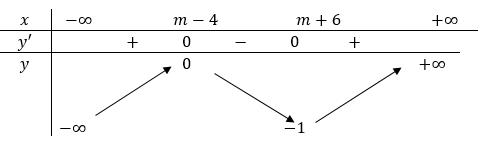
Cho hàm số y=f(x). Hàm số y=f'(x) có bảng xét dấu:
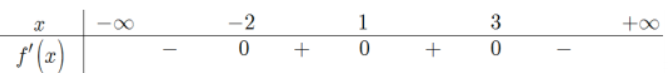
Hàm số \(y=f\left(x^{2}+2 x\right)\) nghịch biến trên khoảng nào dưới đây
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(y^{\prime}=\left(f\left(x^{2}+2 x\right)\right)^{\prime}=(2 x+2) f^{\prime}\left(x^{2}+2 x\right)\)
Hàm số nghịch biến khi \(y^{\prime} \leq 0 \Leftrightarrow(2 x+2) \dot{f}^{\prime}\left(x^{2}+2 x\right) \leq 0\)
TH1:
\(\left\{\begin{array}{l} 2x+2 \leq 0 \\ f^{\prime}\left(x^{2}+2 x\right) \geq 0 \end{array} \Leftrightarrow\left\{\begin{array}{l} x \leq-1 \\ -2 \leq x^{2}+2 x \leq 3 \end{array} \Leftrightarrow\left\{\begin{array}{l} x \leq-1 \\ -3 \leq x \leq 1 \end{array} \Leftrightarrow-3 \leq x \leq-1\right.\right.\right.\)
TH2:
\(\left\{\begin{array}{l} x+1 \geq 0 \\ f^{\prime}\left(x^{2}+2 x\right) \leq 0 \end{array}\right.\)\(\Leftrightarrow\left\{\begin{array}{l} x \geq-1 \\ {\left[\begin{array}{l} x^{2}+2 x \leq-2\text{( vô nghiệm )} \\ x^{2}+2 x \geq 3 \end{array}\right.} \end{array}\right.\)\(\Leftrightarrow\left\{\begin{array}{l} x \geq-1 \\ x \leq-3 \vee x \geq 1 \end{array} \Leftrightarrow x \geq 1\right.\)
Vậy hàm số nghịch biến trên mỗi khoảng \((-3 ;-1) \text { và }(1 ;+\infty)\)
Suy ra hàm số nghịch biến trên (- 2; -1).Chọn đáp án C