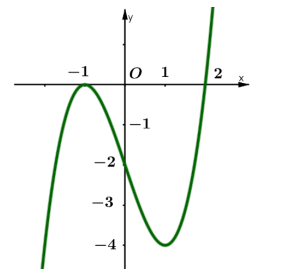
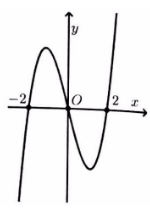
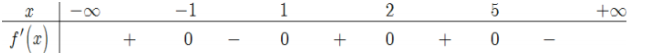Cho hàm số y =f(x) có bảng biến thiên như sau:

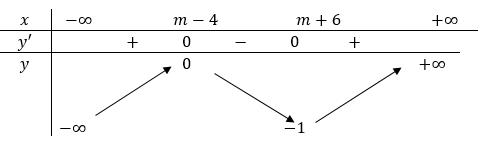
Có bao nhiêu số nguyên \(m \in(-40 ; 40)\) để hàm số \(\mathrm{y}=\mathrm{f}\left(\mathrm{x}^{2}\right)\) đồng biến trên khoảng \((2 ;+\infty)\)

 

Câu hỏi liên quan

• Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất.

• Hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 1\) đồng biến trên khoảng nào sau đây?

• Hàm số \(y = {x^3} - 5{x^2} + 5\) nghịch biến trên khoảng nào sau đây?

ZUNIA12

• Cho hàm số f(x) có đạo hàm \(f'\left( x \right)\; = \;\sqrt {x\left( {x - 1} \right){{\left( {x + 2} \right)}^2}} \)

  Kết luận nào sau đây là đúng?

• Hàm số \(y = {x^3} - 3{x^2} + 1\) đồng biến trên khoảng nào sau đây?

• Tìm m để hàm số \(y=-x^{3}+3 x^{2}+3 m x-1\) nghịch biến trên \((0;+\infty)\)

• Với giá trị nào của m thì hàm số \(y = \frac{{sinx - m}}{{\sin x + m}}\) đồng biến trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\)?

• Giá trị của tham số m để \(f(x)=2 m x^{3}-6 x^{2}+(2 m-4) x+3+m\) nghịch biến trên R là? 

• Hàm số nào sau đây có bảng biến thiên như hình dưới?

  

• Hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVC0xf9qq1qpepC0xbbL8F4rqGqFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaciaabeqaamaabiabcaGcbaaeaaaaaaaaa8 % qacaWG5bGaeyypa0JaeyOeI0IaamiEa8aadaahaaWcbeqaa8qacaaI % 0aaaaOGaey4kaSIaaGioaiaadIhapaWaaWbaaSqabeaapeGaaGOmaa % aakiabgUcaRiaaiAdaaaa!3FD9! y = - {x^4} + 8{x^2} + 6\) đồng biến trên khoảng nào dưới đây?

• Tìm số nguyên m nhỏ nhất sao cho hàm số \(y=\frac{(m+3) x-2}{x+m}\) luôn nghịch biến trên các khoảng xác định của nó?
   

• Cho hàm số \(y\; = \;{x^3}\; + \;3{x^2}\; - \;9x\; + \;15\). Khẳng định nào sau đây là khẳng định sai?

• Cho hàm số y=f(x) có bảng biến thiên như sau

  
  Hàm số \(y=f\left(x^{2}-2\right)\) nghịch biến trên khoảng nào dưới đây

•  Hàm số \(y = - 2{x^3} + 3{x^2} - 3\) đồng biến trên các khoảng: 

• Cho hàm số đa thức f (x) có đạo hàm tràm trên R . Biết f(0)=0  và đồ thị hàm số \(y=f^{\prime}(x)\) như hình sau.

  
  Hàm số \(g(x)=\left|4 f(x)+x^{2}\right| \) đồng biến trên khoảng nào dưới đây 

• Hàm số \(y = \frac{2}{{{x^2} + 1}}\) nghịch biến trên khoảng nào dưới đây?

• Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây?

  

• Cho hàm sô y=f(x) có xác định, liên liên tục trên [-2;2] và có đồ thị là đường cong như hình vẽ bên. Khẳng định nào sau đây là đúng?

  

• Cho hàm số \(y = \frac{{2x + 1}}{{x + 1}}\). Tìm mệnh đề đúng

• Cho hàm số y = x⁴ – 2x² – 3. Khẳng định nào sau đây là sai?