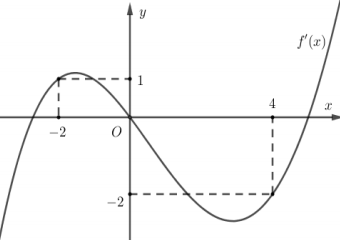
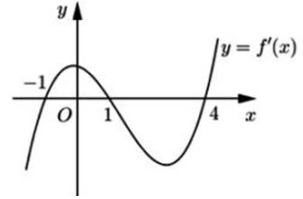
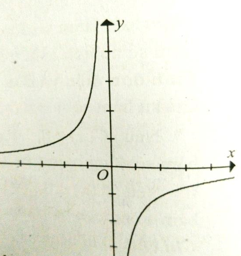
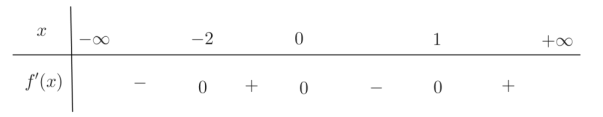Cho hàm số y=f(x) có đạo hàm trên \(\mathbb{R}\) và có đồ thị hàm số y=f'(x) như hình vẽ.
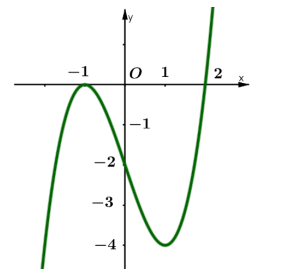
Đặt \(g(x)=f\left(x^{2}-2\right)\) Mệnh đề nào dưới đây sai?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có \(g^{\prime}(x)=2 x f^{\prime}\left(x^{2}-2\right)\)
\(g'(x)=2 x f^{\prime}\left(x^{2}-2\right)>0 \Leftrightarrow\)\(\left[\begin{array}{l} \left\{\begin{array}{l} x>0 \\ f^{\prime}\left(x^{2}-2\right)>0 \end{array}\right. \\ \left\{\begin{array}{l} x<0 \\ f^{\prime}\left(x^{2}-2\right)<0 \end{array}\right. \end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{l} \left\{\begin{array}{l} x>0 \\ x^{2}-2>2 \end{array}\right. \\ \left\{\begin{array}{l} x<0 \\ x^{2}-2<2 \end{array}\right. \end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{l} x>2 \\ -2<x<0 \end{array}\right.\)
vậy hàm số đồng biến trên \((2 ;+\infty)\) nên A đúng
Hàm số đồng biến trên (-2;0) nên cũng đồng biến trên (-1;0).
Vậy C sai.