Cho hàm số y=f(x) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
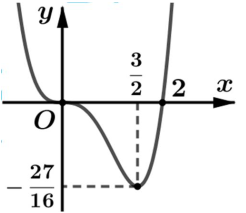
Có bao nhiêu giá trị nguyên của tham số m để phương trình \(f(2|\sin x|)=f\left(\frac{m}{2}\right)\) có đúng 12 nghiệm phân biệt thuộc đoạn \([-\pi ; 2 \pi] ?\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
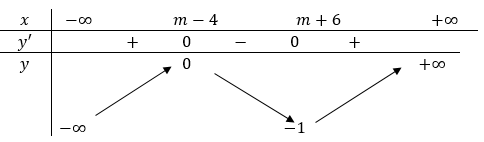
Báo saiTa có bảng biến thiên của hàm số \(y=g(x)=2|\sin x|\) trên đoạn \([-\pi ; 2 \pi]\)
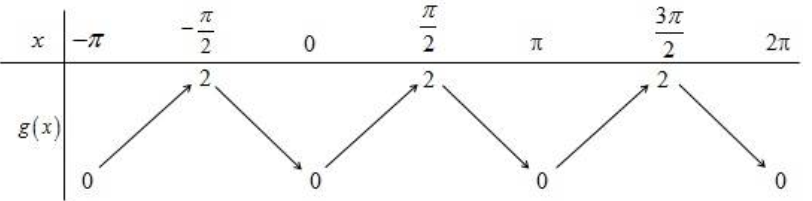
Đặt \(t=2|\sin x|\), \(t \in(0 ; 2)\)
Phương trình \(f(2|\sin x|)=f\left(\frac{m}{2}\right)\) có đúng 12 nghiệm phân biệt thuộc đoạn \([-\pi ; 2 \pi]\) khi và chỉ khi phương trình \(f(t)=f\left(\frac{m}{2}\right)\) có 2 nghiệm phân biệt \(t \in(0 ; 2)\) . Dựa vào đồ thị hàm số y=f(t) suy ra phương trình \(f(t)=f\left(\frac{m}{2}\right)\) có 2 nghiệm phân biệt \(t \in(0 ; 2)\) khi và chỉ khi
\(-\frac{27}{16}