Cho hàm số y =f(x) có đồ thị của hàm số\(y=f^{\prime}(x) \) như hình vẽ bên. Hàm số \(y=f\left(3-x^{2}\right)\) đồng biến trên khoảng
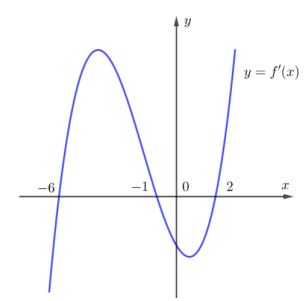
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiHàm số đồng biến \(\Leftrightarrow y^{\prime}=-2 x f^{\prime}\left(3-x^{2}\right)>0 \Leftrightarrow x f^{\prime}\left(3-x^{2}\right)<0\)
Với \(x>0 \Rightarrow f^{\prime}\left(3-x^{2}\right)<0 \Leftrightarrow\left[\begin{array}{l} 3-x^{2}<-6 \\ -1<3-x^{2}<2 \end{array}\right.\)\(\Leftrightarrow \left[\begin{array}{l} x>3 \\ 1<x<2 \end{array}\right.\)
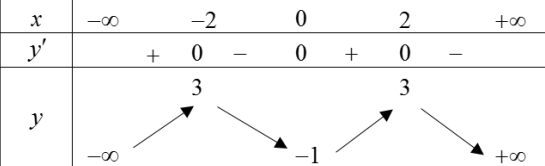
Với \(x<0 \Rightarrow f^{\prime}\left(3-x^{2}\right)>0 \Leftrightarrow\left[\begin{array}{l} -6<3-x^{2}<-1 \\ 3-x^{2}>2 \end{array} \Leftrightarrow \quad\left[\begin{array}{l} -1<x<0 \\ -3<x<-2 \end{array}\right.\right.\)
Chọn D

.png)











