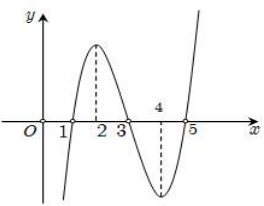
Hàm số y=f(x) có đồ thị hàm số y=f'(x) như hình vẽ. Hỏi đồ thị hàm số \(y=f(2x^2+1)\) đồng biến trong khoảng nào dưới đây?

Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTừ đồ thị hàm số y=f'(x), hàm số y=f(x) đồng biến trên các khoảng \((-1;+\infty)\). Suy ra \(f'(x)>0\Leftrightarrow x>-1\) và \(f'(x)<0\Leftrightarrow x<-1\).
Xét hàm số \(y=f(2x^2+1)\Rightarrow y'=4x.f'(2x^2+1)\).
Hàm số \(y=f(2x^2+1)\) đồng biến khi và chỉ khi \(y'=4x.f'(2x^2+1)>0\)
\( \Leftrightarrow \left[ \begin{array}{l} \left\{ \begin{array}{l} x > 0\\ f'\left( {2{x^2} + 1} \right) > 0 \end{array} \right.\\ \left\{ \begin{array}{l} x < 0\\ f'\left( {2{x^2} + 1} \right) < 0 \end{array} \right. \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} \left\{ \begin{array}{l} x > 0\\ 2{x^2} + 1 > - 1 \end{array} \right.\\ \left\{ \begin{array}{l} x < 0\\ 2{x^2} + 1 < - 1 \end{array} \right. \end{array} \right. \Leftrightarrow x > 0\)