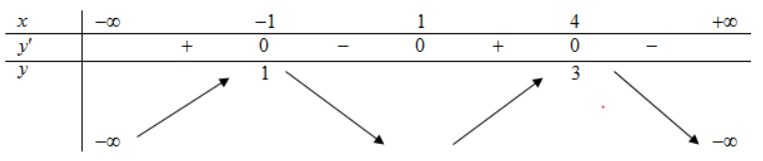
Cho hàm số y=(x) có đạo hàm \(f'(x)=x^{2}(x-1)\left(x^{2}-4\right)\). Hàm số \(y=f(2-x)\) đồng biến trên khoảng
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiTa có \(y^{\prime}=f^{\prime}(2-x)=- f^{\prime}(2-x)=- (2-x)^{2}(2-x-1)\left((2-x)^{2}-4\right)\)
Do đó \(y^{\prime}=-(2-x)^{2}(1-x)\left(x^{2}-4 x\right)\)
Hàm số đồng biến khi \(y^{\prime}>0 \Leftrightarrow(x-1)(x-2)^{2}\left(x^{2}-4 x\right)>0 \Leftrightarrow\left[\begin{array}{l} 0<x<1 \\ x>4 \end{array}\right.\)
Vậy, từ các đáp án đã cho ta có hàm số đồng biến trên khoảng (0;1)
ADMICRO
YOMEDIA
ZUNIA9