Cho hình chóp S ABCD . có đáy là hình chữ nhật với \(A B=a, B C=2 a\) . Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt đáy (ABCD), cạnh \(S A=a \sqrt{15}\). Thể tích của khối chóp đã cho bằng
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai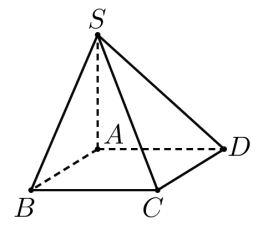
Vì hai mặt bên (SAB) và (SAD) cùng vuông góc với (ABCD), suy ra giao tuyến SA vuông góc với (ABCD).
Do đó chiều cao khối chóp là: \(S A=a \sqrt{15}\).
Diện tích hình chữ nhật: \(S_{A B C D}=A B \cdot B C=2 a^{2}\)
Vậy thể tích khối chóp \(V_{S . A B C D}=\frac{1}{3} S_{A B C D} . S A=\frac{2 a^{3} \sqrt{15}}{3}\)
ADMICRO
YOMEDIA
ZUNIA9











