Cho hình chóp tứ giác đều \(S.ABCD.\) Gọi A', B', C', D' theo thứ tự là trung điểm của AB, BC, CD, \(DA.\) Khi đó tỉ số thể tích của hai khối chóp S.A'B'C'D' và S.ABCD bằng ?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai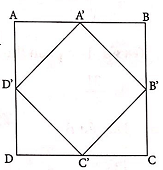
Ta thấy 2 hình chóp S.ABCD và S.A'B'C'D'. Có chung chiều cao kẻ từ đỉnh S xuống đáy. Vậy để đi tìm tỉ số khoảng cách thì chúng ta chỉ cần tìm tỉ số diện tích 2 đáy mà ta có hình vẽ như sau:
Ta thấy
\({{S}_{A'B'C'D'}}=A'D'.A'B'={{\left( \frac{a\sqrt{2}}{2} \right)}^{2}}=\frac{{{a}^{2}}}{2}=\frac{1}{2}{{S}_{ABCD}}\)\(\Rightarrow \frac{{{V}_{A'B'C'D'}}}{{{V}_{ABCD}}}=\frac{1}{2}\)
Câu hỏi liên quan
-
Một hình chóp tam giác có đường cao bằng 100cm và các cạnh đáy bằng \(18cm,\,\,24cm,\,\,30cm.\) Thể tích của khối chóp bằng.
-
Cho khối chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy và khoảng cách từ A đến mặt phẳng (SBC) bằng \(\frac{a \sqrt{2}}{2}\) Thể tích của khối chóp đã cho bằng
-
Cho khối hộp \(ABCD.A'B'C'D'\) có độ dài cạnh bên bằng a; đáy là hình thoi, diện tích của hai mặt chéo là \({{S}_{1}}\) và \({{S}_{2}}\); góc giữa hai mặt phẳng chứa hai mặt chéo là \(\alpha .\) Tính thể tích V của khối hộp đã cho.
-
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với đáy và AB = a, AC = 2a,SA = 3a. Tính thể tích khối chóp S.ABC.
-
Cho hình lăng trụ \(A B C \cdot A^{\prime} B^{\prime} C^{\prime}\) có đáy là tam giác đều cạnh \(2 a \sqrt{2}\) và \(A^{\prime} A=a \sqrt{3}\). Hình chiếu vuông góc của điểm A' trên mặt phẳng (ABC) trùng với trọng tâm G của tam giác ABC. Thể tích của khối lăng trụ đã cho bằng
-
Cho hình chóp tứ giác S.ABCD có thể tích bằng V với đáy là hình bình hành. Gọi C’ là trung điểm cạnh SC. Mặt phẳng qua AC’ và song song với BD cắt các cạnh SB,SD lần lượt tại B’; D’. Khi đó thể tích của khối chóp S.A’B’C’D’ bằng
-
Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, biết A'A = A'B = A'C = a. Tính thể tích khối lăng trụ ABC.A'B'C'.
-
Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, góc \(\widehat{B A D}=120^{\circ}\) Cạnh bên SA vuông góc với mặt phẳng đáy, cạnh bên SD tạo với mặt phẳng đáy một góc\(60^{0}\) Thể tích của khối chóp đã cho bằng
-
Khối hộp chữ nhật ABCD.A’B’C’D' có AB = a, diện tích của ABCD và ABC’D’ lần lượt bằng \(2{a^2}\) và {a^2}\sqrt 5 \). Thể tích khối chữ nhật bằng.
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc mặt đáy, \(SA = a\sqrt 6 \). Tính thể tích khối chóp S.ABCD.
-
Cho hình chóp S ABCD . có đáy là hình chữ nhật với \(A B=a, B C=2 a\) . Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt đáy (ABCD), cạnh \(S A=a \sqrt{15}\). Thể tích của khối chóp đã cho bằng
-
Cho hình lăng trụ tứ giác ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a và thể tích bằng 3a3. Tính chiều cao h của hình lăng trụ đã cho.
-
Cho khối chóp S.ABC có SA vuông góc với mặt đáy,\(S A=4, \quad A B=6, \quad B C=10 \text { và } C A=8\) . Thể tích của khối chóp đã cho bằng
-
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, cạnh bên SB vuông góc với đáy (ABC), SB = 2a. Tính thể tích khối chóp S.ABC.
-
Thể tích khối chóp có độ dài đường cao bằng 6, diện tích đáy bằng 8 là
-
Cho hình chóp S.ABC biết \(AB = 8,\,\,BC = 4,\widehat {\,ABC} = {60^0}\). Hình chiếu của S lên cạnh AB là điểm K sao cho KB = 3KA. Biết \(SB,\,SC\) cùng hợp với đáy một góc \({60^0}\). Tính thể tích khối chóp S.ABC.
-
Cho khối chóp tứ giác \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, \(M\) là trung điểm cạnh \(SC\) và \(N\) là điểm thuộc cạnh \(SD\) sao cho \(SN=2ND\). Tính tỉ số thể tích \(k\) giữa hai đa diện \(SABMN\) và khối chóp \(S.ABCD.\)
-
Cho hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại B, \(AB=a, BC=2a\). Tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với đáy. Gọi \(G\) là trọng tâm tam giác \(ABC\), mặt phẳng \(\left( SAG \right)\) tạo với đáy một góc \(60{}^\circ \). Thể tích khối tứ diện \(ACGS\) bằng
-
Cho một tấm nhôm hình chữ nhật ABCD có \(AD=60cm\). Ta gấp tấm nhôm theo 2 cạnh MN và PQ vào phía trong đến khi AB và DC trùng nhau như hình vẽ dưới đây để được một hình lăng trụ khuyết 2 đáy. Tìm x để thể tích khối lăng trụ lớn nhất?
.png)
-
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = 2a, SC = 3a. Thể tích khối chóp S.ABC là
