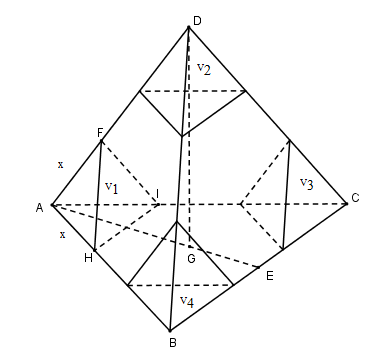
Cho tứ diện đều ABCD có cạnh bằng 8. Ở bốn đỉnh tứ diện, nguời ta cắt đi các tứ diện đều bằng nhau có cạnh bằng x, biết khối đa diện tạo thành sau khi cắt có thể tích bằng \( \frac{3}{4}\) thể tích tứ diện ABCD. Giá trị của x là:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Tứ diện ABCD đều cạnh a có thể tích là \( {V_{ABCD}} = \frac{{{a^3}\sqrt 2 }}{{12}}\)
Vì tứ diện đều ABCD cạnh 8 nên \( {V_{ABCD}} = \frac{{{8^3}\sqrt 2 }}{{12}} = \frac{{128\sqrt 2 }}{3}\)
Tứ diện đều FAHI cạnh x nên \( {V_1} = \frac{{{x^3}\sqrt 2 }}{{12}}\)
Tương tự ta có: \({V_2} = {V_3} = {V_4} = \frac{{{x^3}\sqrt 2 }}{{12}}\)
⇒ Khối đa diện tạo thành sau khi cắt có thể tích là \( V = {V_{ABCD}} - 4{V_1} = \frac{{128\sqrt 2 }}{3} - 4\frac{{{x^3}\sqrt 2 }}{{12}} = \frac{{\left( {128 - {x^3}} \right)\sqrt 2 }}{3}\)
Vì khối đa diện tạo thành sau khi cắt có thể tích bằng \( \frac{3}{4}\) thể tích tứ diện BCD nên ta có:
\( \frac{{\left( {128 - {x^3}} \right)\sqrt 2 }}{3} = \frac{3}{4}\frac{{128\sqrt 2 }}{3} \Rightarrow 128 - {x^3} = 96 \Leftrightarrow {x^3} = 32 \Rightarrow x = \sqrt[3]{{32}} = 2\sqrt[3]{4}\)
Đáp án cần chọn là: D
Câu hỏi liên quan
-
Khối 20 mặt đều là khối đa diện đều thuộc loại nào?
-
Trong các mệnh đề sau, mệnh đề nào sai?
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, \(SD = \frac{{a\sqrt {23} }}{2}\) . Hình chiếu vuông góc của SS lên mặt phẳng (ABCD) là trung điểm H của đoạn AB. Thể tích của chóp S.ABCD là
-
Khối 12 mặt đều có bao nhiêu đỉnh ?
-
Khối đa diện đều loại {5;3} có tên gọi là:
-
Khối đa diện đều loại (3;4) có tất cả bao nhiêu cạnh?
-
Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?
-
Khối đa diện đều nào sau đây có mặt không phải là tam giác đều?
-
Trong các hình đa diện đều sau, hình nào có số đỉnh nhỏ hơn số mặt?
-
Điền vào chỗ trống cụm từ nào cho dưới đây để được một mệnh đề đúng?
“Tồn tại hình đa diện đều mà các mặt của nó là những….”
-
Trong các hình dưới đây hình nào không phải đa diện lồi?
-
Khối bát diện là khối đa diện đều thuộc loại nào?
-
Tính thể tích V của khối chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = 3a, BC = 5a, SA = \(2a\sqrt 3 ,\widehat {SAC} = {30^0}\) và mặt phẳng (SAC) vuông góc mặt đáy.
-
Khối bát diện đều có bao nhiêu cạnh?
-
Hình vẽ sau đây là hình trải phẳng của khối đa diện đều nào?
-
Xác định m để bốn điểm A(1;−1;0),B(−1;2;3),C(2;2;1),D(m;3;5) tạo thành một tứ diện
-
Khối đa diện đều có 20 mặt thì có bao nhiêu cạnh?
-
Cho phép vị tự tâm (O ) tỉ số (k < 0 ) lần lượt biến điểm (M,N ) thành (M',N' ), chọn mệnh đề sai:
-
Mệnh đề nào dưới đây sai?
-
Hình hộp ABCD.A′B′C′D′ có A(0;0;1), B(−1;1;0),D(−2;−1;0), A′(1;1;0). Tọa độ đỉnh C′ là
