Có bao nhiêu giá trị nguyên âm của tham số m để hàm số \(y = {x^3} + mx - \frac{1}{{5{x^5}}}\) đồng biến với x > 0?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai+ Hàm số xác định và liên tục với mọi x> 0.
Ta có
+ Hàm số đồng biến trên khoảng (0; +∞) khi và chỉ khi \(y' = 3{x^2} + m + \frac{1}{{{x^6}}} \ge 0\) với mọi x > 0.
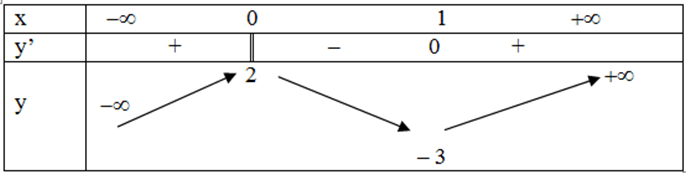
Bảng biến thiên
Suy ra maxg( x) = g(1) = - 4 và do đó để hàm số đã cho đồng biến t với x > 0 thì m ≥ -4
Mà m nguyên âm nên {−4;−3;−2;−1}.
ADMICRO
YOMEDIA
ZUNIA9
.png)











