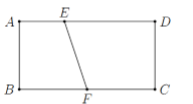
Có một miếng bìa hình chữ nhật (ABCD ) với AB = 3 và AD = 6. Trên cạnh (AD ) lấy điểm (E ) sao cho (AE = 2 ), trên cạnh (BC ) lấy điểm (F ) là trung điểm của BC. Cuốn miếng bìa lại sao cho (AB ) trùng (DC )để tạo thành mặt xung quanh của một hình trụ. Khi đó tính thể tích (V ) của tứ diện (ABEF ).
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Dựng hình lăng trụ (như hình vẽ).
\(\begin{array}{*{20}{l}} {{V_{ABEF}} = \frac{1}{2}{V_{F.AEMB}} = \frac{1}{2}\left( {{V_{AEN.BMF}} - {V_{F.AEN}}} \right) = \frac{1}{2}.\left( {{V_{AEN.BMF}} - \frac{1}{3}{V_{AEN.BMF}}} \right)}\\ { = \frac{1}{2}.\frac{2}{3}{V_{AEN.BMF}} = \frac{1}{3}{V_{AEN.BMF}}} \end{array}\)
ΔAEN vuông tại E có \( AN = 2R = \frac{{AD}}{\pi } = \frac{6}{\pi }\)
Số đo góc \( \widehat {ANE} = \frac{1}{2}.\frac{1}{3}{.360^0} = {60^0}\)
⇒ ΔAEN là một nửa tam giác đều cạnh
\(\begin{array}{l} \frac{6}{\pi } \Rightarrow {S_{{\rm{\Delta }}AEN}} = \frac{1}{2}.\frac{{{{\left( {\frac{6}{\pi }} \right)}^2}\sqrt 3 }}{4} = \frac{{9\sqrt 3 }}{{2{\pi ^2}}}\\ \Rightarrow {V_{AEN.BMF}} = 3.\frac{{9\sqrt 3 }}{{2{\pi ^2}}} = \frac{{27\sqrt 3 }}{{2{\pi ^2}}} \Rightarrow {V_{ABEF}} = \frac{{9\sqrt 3 }}{{2{\pi ^2}}} \end{array}\)
Câu hỏi liên quan
-
Cho hình nón có bán kính đáy bằng 4a và chiều cao bằng 3a. Diện tích toàn phần của hình nón bằng:
-
Trong không gian, cho tam giác ABC vuông tại A có AB = 3, AC = 4. Tính diện tích toàn phần Stp của hình nón khi quay tam giác ABC xung quanh trục AC.
-
Hình trụ (H) có tỉ số diện tích xung quanh và diện tích toàn phần là 1/3. Biết rằng thể tích khối trụ là 4π. Bán kính đáy của hình trụ là:
-
Một hình trụ có diện tích xung quanh là (\(16\pi \)), thiết diện qua trục là hình vuông. Một mặt phẳng ( \(\alpha \)) song song với trục, cắt hình trụ theo thiết diện là (ABB'A' ), biết một cạnh thiết diện là một dây của đường tròn đáy hình trụ và căng một cung 1200. Chu vi tứ giác (ABB'A' ) bằng:
-
Cho hình chữ nhật ABCD có AB = 3,BC = 4. Gọi V1,V2 lần lượt là thể tích của các khối trụ sinh ra khi quay hình chữ nhật quanh trục AB và BC. Khi đó tỉ số \( \frac{{{V_1}}}{{{V_2}}} \)
-
Cho khối nón có bán kính đáy r = 2, chiều cao \(h = \sqrt 3 .\) Thể tích của khối nón là
-
Cho hình lăng trụ có đường kính đáy bằng 6cm , độ dài đường cao bằng 4cm . Tính diện tích xung quanh của hình trụ này
-
Cho hình (H) dưới đây: Quay hình (H) quanh trục đối xứng của nó ta được:
-
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên 2a. Thể tích khối cầu ngoại tiếp khối chóp trên là
-
Cho hình trụ có các đáy là hai hình tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng \(a.\) Trên đường tròn đáy tâm O lấy điểm A, trên đường đáy tâm O’ lấy điểm B sao cho \(AB=2a.\) Tính thể tích của khối tứ diện \(\text{OO}'AB.\)
-
Cho hình nón có đường cao h = 10cm và thiết diện cắt bởi mặt phẳng qua trục của hình nón là một tam giác đều. Diện tích xung quanh của hình nón là:
-
Cho hình nón tròn xoay có đường cao h = 15cm và bán kính đáy r = 20cm. Diện tích xung quanh của hình nón là:
-
Số hình nón có được khi quay hình sau quanh trục (BC ) là:
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, tam giác SAB đều cạnh a và nằm trong mặt phẳng vuông góc với đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD theo a.
-
Cho hình trụ có trục (\(\Delta \)) và bán kính (R ). Khi cắt hình trụ bởi mặt phẳng (\(\alpha \)) song song với (\(\Delta \)) và cách (\(\Delta\) ) một khoảng \(d( \Delta ;(\alpha) ) = k < R \) thì ta được thiết diện là:
-
Cho hình chữ nhật (ABCD ), khi quay hình chữ nhật quanh cạnh (AB ) thì (CD ) được gọi là:
-
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2 và cạnh bên bằng \(2\sqrt3\) . Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABC
-
Mệnh đề nào sau đây là sai?
-
Cho hình nón có bán kính đáy và đường cao lần lượt là r = 6cm,h = 8cm. Tính diện tích toàn phần của hình nón.
-
Một hình nón có đường sinh bằng \(l\) và bằng đường kính đáy. Bán kính hình cầu nội tiếp hình nón bằng:
