Tìm tất cả các giá trị thực k đề phương trình \(\left| { - 2{x^3} - \frac{3}{2}{x^2} + 3x + \frac{1}{2}} \right| = \left| {\frac{k}{2} - 1} \right|\) có đúng 4 nghiệm phân biệt.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
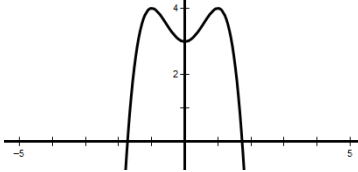
Báo sai+ Đặt \(f\left( x \right)\; = \; - 2{x^3} - \frac{3}{2}{x^2} + 3x + \frac{1}{2}\)
+ Đạo hàm f’(x) = -6x2-3x+ 3 và f’(x) = 0 ⇔ x = -1 hoặc x = 1/2
+ Suy ra đồ thị của hàm trị tuyệt đối \(y = 3\left| { - 2{x^3} - \frac{3}{2}{x^2} + 3x + \frac{1}{2}} \right|\) bằng cách lấy đối xứng qua trục Ox
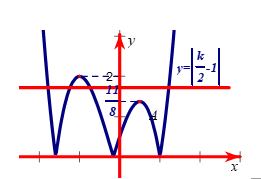
Vậy để PT có đúng 4 nghiệm phân biệt
\(\begin{array}{l}
\Leftrightarrow \frac{{11}}{8} < \left| {\frac{k}{2} - 1} \right| < 2\; \Leftrightarrow \frac{{121}}{{64}} < \frac{{{k^2}}}{4} - k + 1 < 4\\
\Leftrightarrow \left\{ \begin{array}{l}
\frac{{{k^2}}}{4} - k - \frac{{57}}{{64}} > 0\\
\frac{{{k^2}}}{4} - k - 3
\end{array} \right. < 0\\
\Leftrightarrow \left\{ \begin{array}{l}
\left[ \begin{array}{l}
k < - \frac{3}{4}\\
k > \frac{{19}}{4}
\end{array} \right.\\
- 2 < k < 6
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
- 2 < k < - \frac{3}{4}\\
\frac{{19}}{4} < k < 6
\end{array} \right.
\end{array}\)


.jpg.png)
.png)