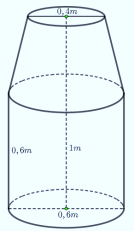
Tính thể tích của thùng đựng nước có hình dạng và kích thước như hình vẽ
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiThể tích của thùng đựng nước là: \({V = {V_1} + {V_2}}\) với \({V_1}\) là thể tích khối trụ có đường kính đáy bằng \(2{R_1} = 0,6\,\,m\) và chiều cao \({h_1} = 0,6\,\,m\); \({V_2}\) là thể tích khối nón cụt có đường kính đáy lớn \(2{R_1} = 0,6\,\,m\) và đường kính đáy nhỏ \(2{R_2} = 0,4\,\,m\) và chiều cao \({h_2} = 1 - 0,6 = 0,4\,\,m\).
Khi đó: \({V_1} = \pi R_1^2.{h_1} = \pi .{\left( {0,3} \right)^2}.0,6 = \frac{{27\pi }}{{500}}\left( {{m^3}} \right)\)
\(\begin{array}{l} {V_2} = \frac{1}{3}\pi {h_2}\left( {{R_1}^2 + {R_2}^2 + {R_1}{R_2}} \right)\\ = \frac{1}{3}\pi .0,4.\left( {0,09 + 0,04 + 0,06} \right) = \frac{{19\pi }}{{750}}\left( {{m^3}} \right) \end{array}\)
Vậy \(V = {V_1} + {V_2} = \frac{{27\pi }}{{500}} + \frac{{19\pi }}{{750}} = \frac{{199}}{{1500}}\pi \left( {{m^3}} \right) = \frac{{0,238\pi }}{3}\left( {{m^3}} \right)\).